|
Question 199466: Hi!
A quadratic function of f is given.
f (x) = 3x^2 + 6x - 7
Find its vertex and its x- and y-intercept(s)
thanks for the homework help!
Found 2 solutions by nerdybill, gracia143:
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! Manipulate your equation into the "vertex form":
y= a(x-h)^2+k
where
(h,k) is the vertex
.
f(x) = 3x^2 + 6x - 7
f(x) = (3x^2 + 6x) - 7
f(x) = 3(x^2 + 2x) - 7
Complete the square:
f(x) = 3(x^2 + 2x + 1) - 7 - 3
f(x) = 3(x+1)^2 - 10
.
Therefore, the vertex is:
(h,k) = (-1, -10)
.
To find the y-intercepts, set x=0 and solve for f(x):
f(x) = 3x^2 + 6x - 7
f(x) = 3(0^2) + 6(0) - 7
f(x) = - 7
y-intercept is (0, -7)
.
To find x-intercepts, set f(x)=0 and solve for x:
0 = 3x^2 + 6x - 7
Using the quadratic equation, we get:
x = {0.826, -2.826}
x-intercepts are at:
(-2.826,0) and (0.826,0)
.
Details of quadratic follows:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=120 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 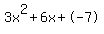 can be factored: can be factored:

Again, the answer is: 0.825741858350554, -2.82574185835055.
Here's your graph:
 |
Answer by gracia143(4)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given: f (x) = 3x^2 + 6x - 7 , where
For the Vertex:
 , X-Intercept (-1,0) , X-Intercept (-1,0)
Subst. x=-1 into the eqn for Y-Intercept:


 , Y-Intercept (0,-10) , Y-Intercept (0,-10)
Vertex @ (-1,-10)
Solving the Quadratic Eqns to find the X-Intercepts of the graph:

Solving for the discriminant: 
Then,



X-Intercepts: (0.825,0) & (-2.825,0)
For Y-Intercept, Let Fx=0:

 , Y-Intercept (0,-7) , Y-Intercept (0,-7)

Thank you,
Jojo
|
|
|
| |