Question 199219: A jar contains a total of 85 coins, all of which are either DIMES OR QUARTERS. If the coins together are worth $15.40, how many of each type of coin are in the jar?
Please help -- can't figure this one out.
Thank you!
Found 2 solutions by Alan3354, ankor@dixie-net.com:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A jar contains a total of 85 coins, all of which are either DIMES OR QUARTERS. If the coins together are worth $15.40, how many of each type of coin are in the jar?
-----------------
D + Q = 85 (# of coins)
10D + 25Q = 1540 (value of coins)
D = 85-Q
Sub for D
10*(85-Q) + 25Q = 1540
850-10Q + 25Q = 1540
15Q = 690
Q = 46
D = 39
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A jar contains a total of 85 coins, all of which are either DIMES OR QUARTERS.
If the coins together are worth $15.40, how many of each type of coin are in the jar?
:
Let d = number of dimes
Let q = number of quarters
;
It says,"A jar contains a total of 85 coins,"; therefore:
d + q = 85
or
d = (85-q); use for substitution
:
"If the coins together are worth $15.40,"; therefore:
.10d + .25q = 15.40
:
Substitute (85-q) for d in the above equation
.10(85-q) + .25q = 15.40
8.5 - .10q + .25q = 15.40
-.10q + .25q = 15.40 - 8.5
.15q = 6.90
q = 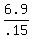
q = 46 quarters
then
d = 85 - 46
d = 39 dimes
;
:
Check solution, find the values
.10(39) + .25(46) =
3.90 + 11.50 = 15.40
|
|
|