Question 198809: Use the following set of values for exercises 8–13.
0.3 0.6 0.9 1.3 0.4 0.6 1.2 1.4 1.1 0.2 0.2
please Find the mean, median, and mode(s) of the data set. Round answers to the nearest hundredth, if necessary.
1. Find the range.
2. Find the interquartile range.
3. Find the standard deviation. Round to the nearest hundredth.
4. Find the 25th and 75th percentiles.
thanks for helping me out!
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! First sort the numbers into ascending order (from least to greatest):
0.2,0.2,0.3,0.4,0.6,0.6,0.9,1.1,1.2,1.3,1.4
Range:
To find the range, subtract the smallest number (in this case 0.2) from the largest number (in this case 1.4) like this:

So the range is 1.2
Interquartile Range:
First, find the median for the first half of the data set (ignore the median):
Median of 0.2, 0.2, 0.3, 0.4, 0.6 is 0.3 (since this is the middle most value)
Now find the median of the last half of the data set (ignore the median):
Median of 0.9, 1.1, 1.2, 1.3, 1.4 is 1.2 (since this is the middle most value)
So the 1st and 3rd quartiles are 0.3 and 1.2 respectively.
This means that the interquartile range is
1.2 - 0.3 = 0.9
Note: the interquartile range is the difference between the 1st and 3rd quartiles
Note: I'm assuming that you want the sample standard deviation.
Standard Deviation:
Step 1) Find the mean:

So the mean is roughly 0.75 (rounded to the nearest hundredth).
----------------------------------------------------------
Step 2) Find the differences between the mean and every value:
Now subtract EVERY value from the mean (0.75) to get:
0.2-0.75 = -0.55, 0.2-0.75 = -0.55, 0.3-0.75 = -0.45, 0.4-0.75 = -0.35, 0.6-0.75 = -0.15, 0.6-0.75 = -0.15, 0.9-0.75 = 0.15, 1.1-0.75 = 0.35, 1.2-0.75 = 0.45, 1.3-0.75 = 0.55, 1.4-0.75 = 0.65,
So you should have a new column of values:
-0.55, -0.55, -0.45, -0.35, -0.15, -0.15, 0.15, 0.35, 0.45, 0.55, 0.65,
----------------------------------------------------------
Step 3) Squaring the differences:
Now square EVERY value in the last column to get:
(-0.55)^2 = 0.3, (-0.55)^2 = 0.3, (-0.45)^2 = 0.2, (-0.35)^2 = 0.12, (-0.15)^2 = 0.02, (-0.15)^2 = 0.02, (0.15)^2 = 0.02, (0.35)^2 = 0.12, (0.45)^2 = 0.2, (0.55)^2 = 0.3, (0.65)^2 = 0.42,
So you should have a new column of values:
0.3, 0.3, 0.2, 0.12, 0.02, 0.02, 0.02, 0.12, 0.2, 0.3, 0.42,
----------------------------------------------------------
Step 4) Adding up the squares:
Now add up the values of the last column:
0.3 + 0.3 + 0.2 + 0.12 + 0.02 + 0.02 + 0.02 + 0.12 + 0.2 + 0.3 + 0.42 = 2.02
----------------------------------------------------------
Step 5) Divide the sum by n-1:
Divide that sum by one less than the number of values in the list (in this case, it is n-1=11-1=10).

----------------------------------------------------------
Step 6) Take the square root of the quotient:
Take the square root of 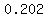 to get to get 
Now round to the nearest hundredth to get  . .
So the standard deviation is roughly  . .
If you don't like that method, then here's another way:
First sort the numbers into ascending order (from least to greatest):
0.2,0.2,0.3,0.4,0.6,0.6,0.9,1.1,1.2,1.3,1.4
Standard Deviation: ^2}) where where  is the average, is the average,  is the ith number, and is the ith number, and  is the number of numbers is the number of numbers
So we can replace N with 11
^2})
Subtract 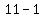 to get 10 to get 10
^2})
Replace  with 0.75 with 0.75
^2})
Expand the summation (replace each  with the respective number) with the respective number)

Subtract the terms in the parenthesis

Square each term

Add up all of the terms
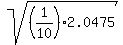
Multiply
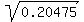
Take the square root
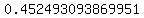
Round to the nearest hundredth

So the standard deviation is roughly 
25th and 75th percentiles:
The 25th and 75th percentiles are simply the first and third quartiles. We found these earlier to be 0.3 and 1.2.
So the 25th and 75th percentiles are 0.3 and 1.2
|
|
|