|
Question 198572: Could someone help me with these, I had it last year but forgot how it works:
1) Find a quadratic equation with roots (4+i)and(4-i).
2) Given the equation x^3-2x^2+x-3=0, what are the possible rational roots??
3) Find the irratinal roots of the equation; x^3-4x^2+2x+1=0 I should use the quadratic formula to solve the equation, it might sound stupid but I never really understood how to use the quadratic formula =(
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!  or or  Start with the given solutions. Start with the given solutions.
 or or  Subtract 4 from both sides (for each equation). Subtract 4 from both sides (for each equation).
 or or  Square both sides Square both sides
 or or  Square i to get -1 and square -i to get -1 Square i to get -1 and square -i to get -1
 or or  Add 1 to both sides. Add 1 to both sides.
Since the equations are the same, we can focus on one equation:

 FOIL FOIL
 Combine like terms. Combine like terms.
So the quadratic with the roots 4+i and 4-i is 
# 2
Any rational zero can be found through this equation
 where p and q are the factors of the last and first coefficients where p and q are the factors of the last and first coefficients
So let's list the factors of -3 (the last coefficient):

Now let's list the factors of 1 (the first coefficient):

Now let's divide each factor of the last coefficient by each factor of the first coefficient

Now simplify
These are all the distinct rational zeros of the function that could occur

# 3
First, let's find the possible rational zeros
Any rational zero can be found through this equation
 where p and q are the factors of the last and first coefficients where p and q are the factors of the last and first coefficients
So let's list the factors of 1 (the last coefficient):

Now let's list the factors of 1 (the first coefficient):

Now let's divide each factor of the last coefficient by each factor of the first coefficient

Now simplify
These are all the distinct rational zeros of the function that could occur

Let's see if the possible zero  is really a root for the function is really a root for the function 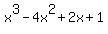
So let's make the synthetic division table for the function 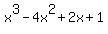 given the possible zero given the possible zero  : :
Since the remainder  (the right most entry in the last row) is equal to zero, this means that (the right most entry in the last row) is equal to zero, this means that  is a zero of is a zero of 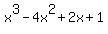
Take note that the first three values in the bottom row are 1, -3, and -1. So this means that

Now all we need to do is solve  to find the next two zeros: to find the next two zeros:
Notice we have a quadratic in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for "x":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Negate Negate  to get to get  . .
 Square Square  to get to get  . .
 Multiply Multiply 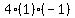 to get to get 
 Rewrite Rewrite 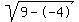 as as 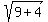
 Add Add  to to  to get to get 
 Multiply Multiply  and and  to get to get  . .
 or or  Break up the expression. Break up the expression.
So the next two zeros are  or or 
===================================================================================
Answer:
So the three roots are  , ,  or or 
where the irrational roots are  and and 
|
|
|
| |