Question 198049: Find the value of the five other trig functions, given sinx=square root -2/2 and cosx<0 also give degree and radian measure of x
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the value of the five other trig functions, given
 and and 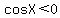 also also
give degree and radian measure of X
I will use a capital X to represent the angle, and a
small x to represent the x-coordinate in the graph.
Don't get them confused!
Since
 and that is a negative number, this tells us that
the angle X is in either QIII of QIV.
Since
and that is a negative number, this tells us that
the angle X is in either QIII of QIV.
Since
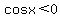 that tells us that the cosine is a negative number,
and we know that the cosine is negative in QII and QIII,
so therefore we know that angle X is in QIII, so we
draw it:
that tells us that the cosine is a negative number,
and we know that the cosine is negative in QII and QIII,
so therefore we know that angle X is in QIII, so we
draw it:
 Since the sine is
Since the sine is  , we take the
numerator of the given sine, which is , we take the
numerator of the given sine, which is  to be the
value of y, and the denominator 2 to be the value of r. to be the
value of y, and the denominator 2 to be the value of r.
 Next we calculate the value of x (small x) using the Pythagorean
theorem:
Next we calculate the value of x (small x) using the Pythagorean
theorem:




 We know to take the velue of x as negative, because
x goes left from the origin, so
We know to take the velue of x as negative, because
x goes left from the origin, so
 and we label it thusly:
and we label it thusly:
 Now we get the other 5 trigonometric functions by using
the definitions:
Now we get the other 5 trigonometric functions by using
the definitions:




 Since the right triangle has two legs equal it is isosceles
are the reference angle is therefore 45°.
Since the angle is in QIII, we must add 180° to its
reference angle, so
the angle X in degree measure is 45°+180° or 225°
In radian measure, we multiply by
Since the right triangle has two legs equal it is isosceles
are the reference angle is therefore 45°.
Since the angle is in QIII, we must add 180° to its
reference angle, so
the angle X in degree measure is 45°+180° or 225°
In radian measure, we multiply by 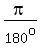
 Edwin
Edwin
|
|
|