SOLUTION: Consider the formula n(A U B) = n(A) + n(B) - n(A ∩ B). (a) Show that this relation holds for A = {1, 2, 3, 4} and B= {2, 4, 5, 6, 7, 8} (b) Make up your own two sets A a

A has 4 elements, so n(A)=4
B has 6 elements, so n(B)=6

A U B = all elements which are in either A or B or both =
{1,2,3,4,5,6,7,8)
A U B has 8 elements so n(A U B) = 8

A ∩ B = all elements which A and B have in common = {2,4}
A ∩ B has 2 elements, so n(A ∩ B) = 2

n(A U B) = n(A) + n(B) - n(A ∩ B).

    8    =  4   +  6   -     2
    8    =      10     -     2
    8    =             8

So it's true.    

(b) Make up your own two sets A and B, each consisting 
of at least six elements. Using these two sets, show 
that the relationship above holds. 

I'll let you do that one by yourself


(c ) Use a Venn diagram and explain why the relation 
holds for any two sets A and B.




The set (circle) A consists of two parts:

and this part

The set (circle) B consists of two parts:

 and this part

Now this part  is common to both sets, so it's A ∩ B

So if we add the number of elements in A to the number
of elements in B, we would have this

n(A) + n(B)

  +    +    +    

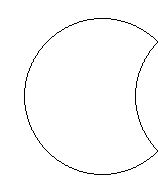But as we see, this amounts to adding this part 

TWICE!!!  This part that we have added twice is A ∩ B.
But we only want to add it ONCE, not TWICE!!!,
So we must subtract the number of elements in A ∩ B ONCE, so
it will not be added TWICE, but only ONCE  

So we subtract it from n(A)+n(B), and we get 

n(A)+n(B)-n(A ∩ B)

and we have this:

  +    +    +    -  

And the set A ∩ B that we subtracted away, cancels with
the extra A ∩ B,

  +    +    +    -  

and we are left with this:

  +    +   
 
which, when we put them back together is this:



which is n(A U B).  That's why the formula works

n(A U B) = n(A) + n(B) - n(A ∩ B),

the n(A ∩ B) gets counted once as part of n(A),
and gets counted again in part of n(B), when we add n(A) + n(B),
and so n(A ∩ B) must be subtracted once to take 
away the extra time it is counted.

Edwin