Question 197703: How can you identify the proper way to follow for the equation?
out of these ways:
1. Square roots - when x^2 is present, when x^2 and x is present
2. graphing
3. factoring
4. quadratic formula
I understand graphing and square roots (somewhat), but when would you use factoring and the quadratic formula? what is the quadratic formula? Can you list the steps of how to do the factoring and quadratic formula? Can you use measures of central tendancy (mean,median,mode) in quadratic functions? Do you have to find the GCF for all of the problems? Would you be able to provide an example problem for when you would factor, and another for when you would use quadratic formula, please?
I am sorry this is so many questions, when you reply can you either do so in complete sentences or with my message above the answers, please?
Thanks, I hope this will help.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Q: Can you use measures of central tendancy (mean,median,mode) in quadratic functions?
A: The mean, median, and mode are totally different concepts compared to the quadratic equation. I don't see you using them in these problems.
-------------
Q: Do you have to find the GCF for all of the problems?
A: You don't have to, but it helps simplify things (sometimes).
------------
As for the other questions, it's probably best to show you examples...
# 1 Square Root Method:
Example: Let's solve 
 Start with the given equation. Start with the given equation.
 Take the square root of both sides to "undo" the square. Take the square root of both sides to "undo" the square.
 or or  Break up the "plus/minus" to form two equations. Break up the "plus/minus" to form two equations.
 or or  Evaluate the square root of 81 to get 9. Evaluate the square root of 81 to get 9.
So the solutions are  or or 
# 2 Graphing
Example: Let's solve  . If we graph . If we graph  , we get: , we get:

Graph of 
From the graph, we see that the curve intersects with the x-axis at  and and  . So the solutions are . So the solutions are  or or 
# 3 Factoring
Example: Let's solve 
First, we need to factor 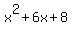
--------------------------------------------------------------------------------
Looking at the expression 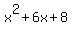 , we can see that the first coefficient is , we can see that the first coefficient is  , the second coefficient is , the second coefficient is  , and the last term is , and the last term is  . .
Now multiply the first coefficient  by the last term by the last term  to get to get  . .
Now the question is: what two whole numbers multiply to  (the previous product) and add to the second coefficient (the previous product) and add to the second coefficient  ? ?
To find these two numbers, we need to list all of the factors of  (the previous product). (the previous product).
Factors of  : :
1,2,4,8
-1,-2,-4,-8
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to  . .
1*8
2*4
(-1)*(-8)
(-2)*(-4)
Now let's add up each pair of factors to see if one pair adds to the middle coefficient  : :
| First Number | Second Number | Sum | | 1 | 8 | 1+8=9 | | 2 | 4 | 2+4=6 | | -1 | -8 | -1+(-8)=-9 | | -2 | -4 | -2+(-4)=-6 |
From the table, we can see that the two numbers  and and  add to add to  (the middle coefficient). (the middle coefficient).
So the two numbers  and and  both multiply to both multiply to  and add to and add to 
Now replace the middle term  with with 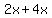 . Remember, . Remember,  and and  add to add to  . So this shows us that . So this shows us that  . .
 Replace the second term Replace the second term  with with 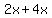 . .
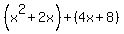 Group the terms into two pairs. Group the terms into two pairs.
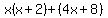 Factor out the GCF Factor out the GCF  from the first group. from the first group.
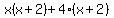 Factor out Factor out  from the second group. The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis. from the second group. The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis.
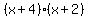 Combine like terms. Or factor out the common term Combine like terms. Or factor out the common term 
So 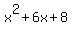 factors to factors to 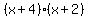 . .
--------------------------------------------------------------------------------
Now let's start solving 
 Start with the given equation. Start with the given equation.
 Factor (see steps above) Factor (see steps above)
 or or  Set each factor equal to zero Set each factor equal to zero
 or or  Solve for "x" in each equation Solve for "x" in each equation
So the solutions are  or or 
# 4 Quadratic Formula
Example: Let's solve 
 Start with the given equation. Start with the given equation.
Notice we have a quadratic in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for "x":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Negate Negate  to get to get  . .
 Square Square  to get to get 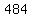 . .
 Multiply Multiply 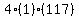 to get to get 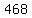
 Subtract Subtract 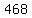 from from 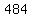 to get to get 
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of  to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the solutions are  or or 
|
|
|