|
Question 196705: I cannot seem to find the correct standard equation, foci, and asymptotes of the following hyperbola:

I need to write it in this kind of form:

I have been solving these kinds of problems wrong lately, and I am quite worried since it will be a subject on an upcoming test. Any help would be appreciated, and many thanks in advance.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! I cannot seem to find the correct standard equation, foci, and asymptotes of the following hyperbola:

Rearrange so that the two terms in x are next to
each other and the two terms in y are next to
each other, and 11 to both sides:
sides:
 The coefficient of
The coefficient of  is already 1, so
we don't factor anything out of it, just enclose the
first two terms in parentheses: is already 1, so
we don't factor anything out of it, just enclose the
first two terms in parentheses:
 Now factor only -4 (not y) out of the last two terms
on the left.
Now factor only -4 (not y) out of the last two terms
on the left.
 Complete the square in each parentheses.
In the first parentheses multiply the
Complete the square in each parentheses.
In the first parentheses multiply the  coefficient of
x by coefficient of
x by  , getting , getting  . Then we square . Then we square  ,
getting ,
getting  . So we add 9 to both sides: . So we add 9 to both sides:

 Now we factor the first parentheses as
Now we factor the first parentheses as 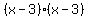 or
or 
 In the second parentheses multiply the
In the second parentheses multiply the  coefficient of
y by coefficient of
y by  , getting , getting  . Then we square . Then we square  ,
getting ,
getting  . So we add 4 inside the second
parentheses.
But since there is a . So we add 4 inside the second
parentheses.
But since there is a  factor in front of the second
parentheses, when we add factor in front of the second
parentheses, when we add  inside the second parentheses
we are really adding inside the second parentheses
we are really adding  times times  or or  to the
left side, so we must add to the
left side, so we must add  to the right side too. to the right side too.

 Now we factor the second parentheses as
Now we factor the second parentheses as  or
or 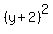
 Next we get a
Next we get a  on the right side by dividing
through by on the right side by dividing
through by 

 Now to get rid of the 4 on top on the second term, we
divide top and bottom by 4
Now to get rid of the 4 on top on the second term, we
divide top and bottom by 4


 Can you go from here?
Compare to
Can you go from here?
Compare to
 So
So  , ,  , ,  , ,  So center = (h,k) = (3,-2)
The two vertices are a=2 units left and right of the
center, so they are (1,-2) and (5,-2)
The two foci are
So center = (h,k) = (3,-2)
The two vertices are a=2 units left and right of the
center, so they are (1,-2) and (5,-2)
The two foci are  units left and right of the center.
First we calculate units left and right of the center.
First we calculate  using using




 So the two foci are
So the two foci are  units left and right of the
center, so they are ( units left and right of the
center, so they are (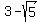 ,-2) and ( ,-2) and (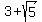 ,-2)
The asymptotes have slopes which are ± ,-2)
The asymptotes have slopes which are ± or
± or
± And the go through the center (3,-2), so we use the
point slope formula:
For the asymptote that has slope
And the go through the center (3,-2), so we use the
point slope formula:
For the asymptote that has slope  : :
 Multiply both sides by 2
Multiply both sides by 2


 ---------------
For the asymptote that has slope
---------------
For the asymptote that has slope  : :
 Multiply both sides by -2
Multiply both sides by -2


 Edwin
Edwin
|
|
|
| |