SOLUTION: Find the roots of the polynomial equation. x^4 - 5x^3 + 11x^2 - 25x + 30 = 0; 2,3

Since you are given that 2 is a root, we
do this synthetic division

2 | 1   -5   11  -25  30
  |      2   -6   10 -30 
   ---------------------
    1   -3    5  -15   0

So now we have factored the original polynomial as



Now we factor the cubic polynomial in 
the 2nd parentheses, using the fact that 3 is
a root of the original, so it must be a 
root of the cubic polynomial in the 2nd
parentheses:

3 | 1 -3  5 -15
  |    3  0  15 
   ---------------
    1  0  5   0

So now we have factored the original polynomial as



or



Setting the first two parentheses = 0 gives
the given two roots, 2 and 3.  To find the
other roots, we set the third factor = 0



Add -5 to both sides



Take the square roots of both sides:





So the roots are 2, 3, , and 

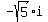Edwin