Question 196647: I keep getting the incorrect answer to the following problem, I'm not sure where my error was, can you help me?
One method for determining the depth of a well is to drop a stone into it and then measure the time it takes until the splash is heard. If d is the depth of the well (in feet) and t1 the time (in seconds) it takes for the stone to fall, then d = 16t1^2, so t1 = √d/4. Now if t2 is the time it takes for the sound to travel back up, then d = 1090t2 because the speed of sound is 1090 ft/s. So t2 = d/1090. Thus, the total time elapsed between dropping the stone and hearing the splash is given by the following equation.
t1 + t2 = √d/4 + d/1090
How deep is the well if this total time is 2.3 s? (Round the answer to the nearest whole number.)
thanks!
Found 2 solutions by jim_thompson5910, Alan3354:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since the "total time is 2.3 s", this means that 
 Start with the given equation. Start with the given equation.
 Plug in Plug in 
 Multiply EVERY term by the LCD Multiply EVERY term by the LCD 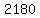 to clear out the fractions. to clear out the fractions.
 Multiply and simplify Multiply and simplify
 Subtract 2d from both sides. Subtract 2d from both sides.
 Square both sides Square both sides
 Square Square  to get to get 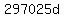
 FOIL the left side FOIL the left side
 Get all terms to the left side. Get all terms to the left side.
 Combine like terms. Combine like terms.
Notice we have a quadratic in the form of 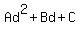 where where  , ,  , and , and 
Let's use the quadratic formula to solve for d
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Negate Negate 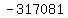 to get to get 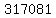 . .
 Square Square 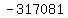 to get to get 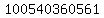 . .
 Multiply Multiply 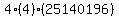 to get to get 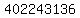
 Subtract Subtract 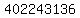 from from 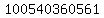 to get to get 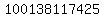
 Multiply Multiply  and and  to get to get  . .
 Simplify the square root (note: If you need help with simplifying square roots, check out this solver) Simplify the square root (note: If you need help with simplifying square roots, check out this solver)
 or or  Break up the expression. Break up the expression.
So the answers are  or or 
which approximate to  or or 
Notice that if the time for the stone to fall was 2.3 seconds, then the depth would be AT MOST  . In other words, the MAX depth that is possible in this problem is about 85 feet. . In other words, the MAX depth that is possible in this problem is about 85 feet.
Since the value  is too large, this means that is too large, this means that  is the only answer. is the only answer.
So to the nearest whole number, the depth of the well is about 79 feet.
Answer by Alan3354(69443)   (Show Source): (Show Source):
|
|
|