SOLUTION: May you please help me with the following hyperbola in standard form: {{{(1/10)(x-1)^2 - (y-1)^2= 1}}} find the center, foci, the length of one of the two axes (transverse or

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: May you please help me with the following hyperbola in standard form: {{{(1/10)(x-1)^2 - (y-1)^2= 1}}} find the center, foci, the length of one of the two axes (transverse or      Log On


   

Question 196562: May you please help me with the following hyperbola in standard form:
%281%2F10%29%28x-1%29%5E2+-+%28y-1%29%5E2=+1
find the center, foci, the length of one of the two axes (transverse or conjugate) which is parallel to the y-axis, and the two asymptotes
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
find the center, foci, the length of one of the two axes (transverse or conjugate) which is parallel to the y-axis, and the two asymptotes.
%281%2F10%29%28x-1%29%5E2+-+%28y-1%29%5E2=+1 


Rewrite that as:

%28%28x-1%29%5E2%29%2F10+-+%28%28y-1%29%5E2%29%2F1+=+1

and compare with

%28%28x-h%29%5E2%29%2Fa%5E2+-+%28%28y-k%29%5E2%29%2Fb%5E2+=+1
 
h+=+1, k=1, 
 
a%5E2=10, so a=sqrt%2810%29
 
b%5E2=1, so b=1
 
The center (h,k) = (1,1)
 
We start out plotting the center C(h,k) = C(1,1)
 

 
Next we draw the left semi-transverse axis,
which is a segment a=sqrt%2810%29 units long horizontally 
left from the center.  This semi-transverse 
axis ends up at one of the two vertices (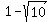1-sqrt%2810%29,1).
                    
We'll call it V1(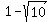1-sqrt%2810%29,1).:
 

 
Next we draw the right semi-transverse axis,
which is a segment a=sqrt%2810%29 units long horizontally 
right from the center. This other semi-transverse
axis ends up at the other vertex (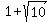1%2Bsqrt%2810%29,1).
We'll call it V2(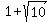1%2Bsqrt%2810%29,1).:
 

 
That's the whole transverse ("trans"="across",
"verse"="vertices", the line going across from
one vertex to the other. It is 2a in length,
so the length of the transverse axis is 2a=2sqrt%2810%29
 
Next we draw the upper semi-conjugate axis,
which is a segment b=1 units long verically 
upward from the center.  This semi-conjugate
axis ends up at (1,2).
 

 
Next we draw the lower semi-conjugate axis,
which is a segment b=1 units long verically 
downward from the center.  This semi-conjugate
axis ends up at (1,0). 


 
That's the complete conjugate axis. It is 2b in length,
so the length of the transverse axis is 2b=2(1)=2
 
Next we draw the defining rectangle which has the
ends of the transverse and conjugate axes as midpoints
of its sides:
 



Next we draw and extend the two diagonals of this defining
rectangle:




Now we can sketch in the hyperbola:
 

 
Next we find the equations of the two asymptotes.
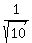Their slopes are ±b%2Fa or ±1%2Fsqrt%2810%29
 
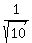The asymptote that has slope 1%2Fsqrt%2810%29 goes through the center
C(1,1), so its equation is found using the point-slope
formula:
 
y-y%5B1%5D=m%28x-x%5B1%5D%29
y-%281%29=%281%2Fsqrt%2810%29%29%28x-1%29%29
y-1=%281%2Fsqrt%2810%29%29%28x-1%29%29

Multiply through by sqrt%2810%29
sqrt%2810%29y-sqrt%2810%29=x-1
-x%2Bsqrt%2810%29y=sqrt%2810%29-1
x-sqrt%2810%29y=-sqrt%2810%29%2B1

The asymptote that has slope -1%2Fsqrt%2810%29 goes through the center
C(1,1), so its equation is also found using the point-slope
formula:
 
y-y%5B1%5D=m%28x-x%5B1%5D%29
y-%281%29=%28-1%2Fsqrt%2810%29%29%28x-1%29%29
y-1=%28-1%2Fsqrt%2810%29%29%28x-1%29%29

Multiply through by sqrt%2810%29
sqrt%2810%29y-sqrt%2810%29=-1%28x-1%29
sqrt%2810%29y-sqrt%2810%29=-x%2B1

x%2Bsqrt%2810%29y=sqrt%2810%29%2B1
x-sqrt%2810%29y=-sqrt%2810%29%2B1
 
All that's left is to find the two foci.

The distance from the vertex, through the center
to each foci is c units. We calculate c from

c%5E2=a%5E2%2Bb%5E2

c%5E2=%28sqrt%2810%29%29%5E2%2B%281%29%5E2

c%5E2=%2810%2B1%29

c%5E2=11

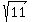c=sqrt%2811%29

So the left focus is sqrt%2811%29 units
left of the center (1,1), so the left
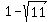focus is the point (1-sqrt%2811%29,1).  That's
just a little left of the vertex V1. And the right
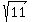focus is sqrt%2811%29 units right of the center
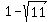(1,1), so the right focus is the point (1-sqrt%2811%29,1).
That's just a little right of the vertex V2. I won't
bother to plot them.

Edwin