SOLUTION: Use the following hyperbola to answer all questions. Find the center, foci, vertices, the length of the transverse and conjugate axis and the asymtotes for the following hyperbol

, , 

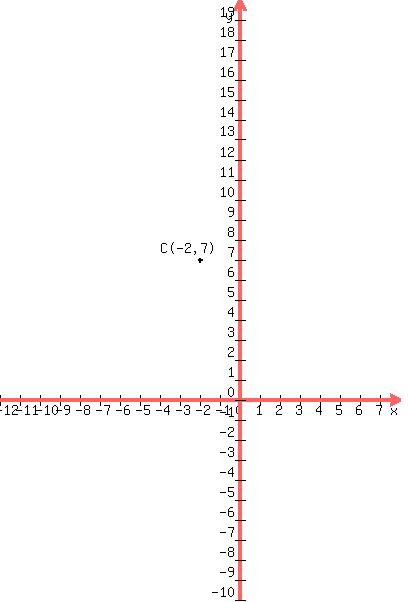
, so 

, so 
 
The center (h,k) = (-2,7)

We start out plotting the center C(h,k) = C(-2,7)



Next we draw the left semi-transverse axis,
which is a segment a=5 units long horizontally 
left from the center.  This semi-transverse
axis ends up at one of the two vertices (-7,7).
We'll call it V1(-7,7):



Next we draw the right semi-transverse axis,
which is a segment a=5 units long horizontally 
right from the center. This other semi-transverse
axis ends up at the other vertex (3,7).
We'll call it V2(3,7):



That's the whole transverse ("trans"="across",
"verse"="vertices", the line going across from
one vertex to the other. It is 2a in length,
so the length of the transverse axis is 2a=2(5)=10

Next we draw the upper semi-conjugate axis,
which is a segment b=8 units long vertically 
upward from the center.  This semi-conjugate
axis ends up at (-2,15).



Next we draw the lower semi-conjugate axis,
which is a segment b=8 units long vertically 
downward from the center.  This semi-conjugate
axis ends up at (-2,-1). 



That's the complete conjugate axis. It is 2b in length,
so the length of the conjugate axis is 2b=2(8)=16

Next we draw the defining rectangle which has the
ends of the transverse and conjugate axes as midpoints
of its sides:



Next we draw and extend the two diagonals of this defining
rectangle:



Now we can sketch in the hyperbola:



All that's left to do is find the equations of the two asymptotes.
Their slopes are ± or ±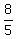

The asymptote that has slope  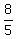goes through the center
C(-2,7), so its equation is found using the point-slope
formula:




Multiply through by 5




The asymptote that has slope  goes through the center
C(-2,7), so its equation is found using the point-slope
formula:




Multiply through by 5




Edwin