Question 195718: A baseball player has hit a ball. The height, y, of the ball x seconds after it is hit is given by y= -16x^2 + 80x + 3.
At what time will the ball reach its maximum height? I used the quadratic formula and my answer was 2.04
What is the maximum height of the ball? I used the original formula.My answer was 232.78
When will the ball hit the ground? My answer was 4.08
Is this right??
thanks
Found 2 solutions by jim_thompson5910, Alan3354:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! At what time will the ball reach its maximum height?
What is the maximum height of the ball?
First, we need the vertex. The vertex will tell us what the max height will be:
In order to find the vertex, we first need to find the x-coordinate of the vertex.
To find the x-coordinate of the vertex, use this formula:  . .
 Start with the given formula. Start with the given formula.
From  , we can see that , we can see that  , ,  , and , and  . .
 Plug in Plug in  and and  . .
 Multiply 2 and Multiply 2 and  to get to get 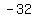 . .
 Reduce. Reduce.
So the x-coordinate of the vertex is  . Note: this means that the axis of symmetry is also . Note: this means that the axis of symmetry is also  . .
Now that we know the x-coordinate of the vertex, we can use it to find the y-coordinate of the vertex.
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Square Square  to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Combine like terms. Combine like terms.
So the y-coordinate of the vertex is  . .
So the vertex is ) . .
which in decimal form is ) . .
So this means that at 2.5 seconds, the ball will be at the max height of 103.
When will the ball hit the ground?
 Start with the given equation. Start with the given equation.
 Plug in Plug in 
Notice we have a quadratic equation in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for x
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get  . .
 Multiply Multiply 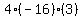 to get to get 
 Rewrite Rewrite 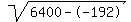 as as 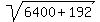
 Add Add  to to  to get to get 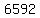
 Multiply Multiply  and and  to get to get 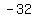 . .
 Simplify the square root (note: If you need help with simplifying square roots, check out this solver) Simplify the square root (note: If you need help with simplifying square roots, check out this solver)
 or or  Break up the expression. Break up the expression.
So the possible answers are  or or 
which approximate to  or or 
Since a negative time doesn't make sense, this means that the only solution is 
So it will take about 5.037 seconds for the ball to hit the ground.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A baseball player has hit a ball. The height, y, of the ball x seconds after it is hit is given by y= -16x^2 + 80x + 3.
At what time will the ball reach its maximum height? I used the quadratic formula and my answer was 2.04
------------------------------
Find the apogee, which is the vertex of the parabola:
hmax = -b/2a
= -80/(-32) = 2.5 seconds
---------------------------
What is the maximum height of the ball? I used the original formula.My answer was 232.78
It's at time = 2.5 seconds.
y = -16*2.5^2 + 80*2.5 + 3
ymax = 103 feet
-----------------
When will the ball hit the ground? My answer was 4.08
Set y = 0
-16x^2 + 80x + 3 = 0
x = 2.5 + (sqrt(103))/4 seconds
x = ~ 5.037222891 seconds
It's not 5 seconds even, because the ball started up from 3' elevation.
|
|
|