Question 194553: A wire 20 feet long is to be cut into two pieces. one pierce will be shaped as a square and the other piece will be shaped as an equilateral triangle. express the total area A enclosed by by the piece of wire as a function of the length x of a side of the equilateral triangle. what is the domain of A? for what value of x will the total area A be the smallest?
please i need help. please help me please.....
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! If  is a side of the equilateral triangle, is a side of the equilateral triangle,
then the length of wire used for the triangle is
 ft ft
The length of wire left over for the square is
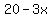 ft ft
One side of that square would be
 ft ft
If  is the total area, then is the total area, then



Multiply both sides by 


-------------------------------------------
If  , or I had no triangle at all, then , or I had no triangle at all, then
 , as it should, since the whole , as it should, since the whole  ft ft
is being used by the squareand 
If  , then nothing is left for the square, and , then nothing is left for the square, and
all the area is used by the triangle.
I'll check this:



 ft2 ft2
and




 ft2 ft2
The domain of  is 19.244 < A < 400 is 19.244 < A < 400
--------------------------------------------
When an equation is of the form
 , the minimum is at , the minimum is at 
In this case,




 ft ft
This is the value of  for which for which  is a minimum is a minimum
I'll graph the function to check this (approximately)

And here's a close-up

|
|
|