Question 19416: I need help with two problems of a problem set of 15. A recent topic I'm unclear on is moment generation functions, I know they can be used to find out probability distributions as well as means and variance but I'm not sure.
a,) Problem 1: suppose that X has a moment generation function m(t)=(.25 + .75e^t)^12. find P(X>4). I know I can differeiate this function and set to zero M(0) but then what do I do?
b. Problem 2: Henry is going to keep rolling a die until he obtains four different values. What is the expected number of rolls that he will need? I have no idea in which to start this problem. My logic is obviously flawed. Help as ASAP. They are due tomorrow a.m. Orignally submitted Friday.
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Problem 1: suppose that X has a moment generation function m(t)=(.25 + .75e^t)^12. find P(X>4).
Comment 1: Never write any function as 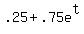 , should be , should be
m(t) = 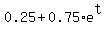
2.Yes, M(0) = 1, M'(0) = E(X) and M"(0) = 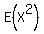
But no differentiation is necessary for solving the pdf P.
3. The point is to know the the MGF of the binomial function B(x,n;p)
is (q + p e^t)^n, where q = 1-p.
[ Since M(t) =  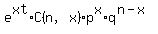 = =  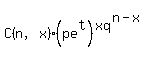
= 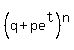 . .
Here, for given m(t) = 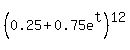 , p=0.75 and , p=0.75 and
the corresponding binomial distribution B(x,n;p) is B(x,12,0.75).
Hence, P(X > 4) = 1 -  B(x,12,0.75) (x = 0,1,2,3) B(x,12,0.75) (x = 0,1,2,3)
= 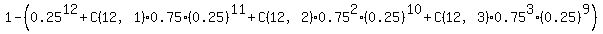
= 0.999608
= 1- BINOMDIST(3,12,0.75,TRUE) (by using Excel)
The next one is difficult for beginners because it should use very high level
formulas in algebra and combinatorials.
Problem 2: Henry is going to keep rolling a die until he obtains four different values. What is the expected number of rolls that he will need?
Sol: 1) Let the corresponding random variable be X.
Of course, we need to compute the pdf of X ,P(X= n), if  first. first.
[Note: P(X= k) = 0 if k <=3]
Note when Henry succeeds (the 4th number) at the nth trial, that means he got exactly 3 distinct numbers in the previous n-1 trials. That is, the same as we consider the sum of all coefficients of the terms of three variables as
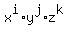 (i,j,k>=1) in the polynomial (i,j,k>=1) in the polynomial 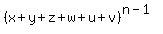 . .
Since there are C(6,3)=20 such triples as xyz in 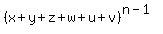 , and there are , and there are  (why?) (why?)
= 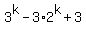 terms of 3 variables in (x+y+z)^k. terms of 3 variables in (x+y+z)^k.
Hence, there are 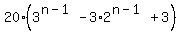 terms of 3 variables terms of 3 variables
(as xyz, yzw,..) in 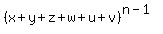 . .
That is among the possible 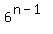 outcomes of first (n-1) rollings, there are outcomes of first (n-1) rollings, there are 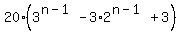 possible appearance of 3 different values. possible appearance of 3 different values.
To be successful(i.e. to make 4 different values), the n th rolling must be one of the remaining 3 numbers. Thus the probability of success at the nth trial is
P(X=n) = 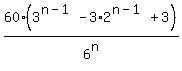 for for 
For example, P(X=4) =  , ,
P(X=5) =  , ,
P(X=6) =  . .
[P must be a pdf, checking ,  P(X=n) = 20* P(X=n) = 20* 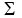  - 90* - 90* 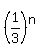 + 180* + 180*  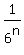 
= 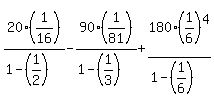
= 
... Correct for a well-defined pdf.]
Therefore, E(X) =  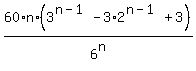
= 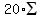 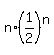 - - 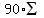 n(1/3)^n + n(1/3)^n +  n/6^n }}} n/6^n }}} 
[Note:   = = 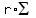 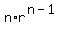 = = 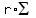 ( (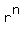 )' = r( )' = r(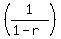 )' = )' = 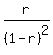 - - 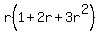 for for 
We obtain E(X) = 20  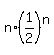 - 90 - 90   + 180 + 180  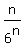
= 
= 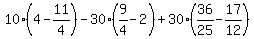
= 5.7
Good luck !!
Kenny
PS 1: I have doubly checked that the answer should be correct.
2. Don't feel bad that you could not do Problem2, but it is a good
exercise for prob. Try to read and understand the above details.
3. You posted these questions in wrong place. I am sure almost nobody
knows what you asked about here.
4. To answer Problem 2, you can write
Let the random variable be X.
(i)Since the the sum of all coefficients of the terms of three variables
in in the polynomial 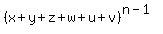 is is
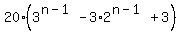
(ii) For  , P(X =n) = , P(X =n) = 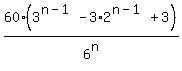
(iii) E(X) =  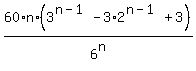
= 5.7
[Using   = =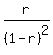 - - 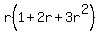
for  ] ]
|
|
|