Question 194150This question is from textbook Saxon Algebra 1
: Please help me solve this equation: 
I tried working it out several times but was unable to understand why the end result was 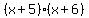 instead of instead of 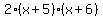 . What happened to the '2', and why and how am I supposed to get rid of it? . What happened to the '2', and why and how am I supposed to get rid of it?
Thank you so much for your help!
This question is from textbook Saxon Algebra 1
Answer by RAY100(1637)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2x^2 + 20x +50 = 0
Let's divide thru each term, on both sides by 2,,,this should not change the expression
x^2 +10x +25 = 0
factor
(x+ 5 ) ( x + 5 ) =0
x+5 = 0, therefore x=-5, and -5,,,,,,,,
checking
2(-5)^2 + 20 (-5) +50 =0
50 -100 +50 = 0
100 = 100,,,,,,ok
,
You were right to be concerned about the (2), but as you see, a constant thruout the
equation, just makes all the numbers larger.
,
Again think of an equation like a balance, or a tee- ter - totter, you can add, subtract, multiply or divide both sides equally, and the balance is maintained.
|
|
|