|
Question 193521This question is from textbook algebra and trigonometry structure and method book 2
: Find the vertex, focus, directrix, and axis of symmetry of each parabola.
x^2+8y+4x-4=0
We have been using the formulas y-k=a(x-h)^2 and x-h=a(y-k)^2 I don't understand which to use here, even after completing the square and its confusing because I don't know which is which. please explain and be specific. thank you.
This question is from textbook algebra and trigonometry structure and method book 2
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Start with the given equation. Start with the given equation.
 Rearrange the terms. Rearrange the terms.
Now we need to complete the square for the "x" terms.
Take half of the x coefficient 4 to get 2. Square 2 to get 4.
 Add the previous result 4 to both sides. Add the previous result 4 to both sides.
 Subtract 4 from both sides. Subtract 4 from both sides.
 Combine like terms. Combine like terms.
 Factor Factor  to get to get 
 Subtract Subtract  from both sides from both sides
 Factor out the GCF 8 from the left side Factor out the GCF 8 from the left side
 Multiply both sides by Multiply both sides by 
 Rewrite Rewrite  as as 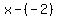
Now the equation  is in the form is in the form  where where  , ,  and and 
Vertex:
The vertex of  is (h,k). Since is (h,k). Since  and and  , the vertex of , the vertex of  is (-2,1) is (-2,1)
-----------------------------------------------------------------------
Focus:
First, we define  where the absolute value of "p" is the distance from the vertex to the focus. where the absolute value of "p" is the distance from the vertex to the focus.
Note: the formula  is derived from the equation is derived from the equation 
The focus of  is the point is the point ) . In other words, simply add the value of "p" to the y coordinate of the vertex to get the focus. . In other words, simply add the value of "p" to the y coordinate of the vertex to get the focus.
So let's find "p":  . So . So 
Since  , ,  , and , and  , this means that , this means that 
So the focus of the form ) is the point (-2,-1) is the point (-2,-1)
------------------------------------------------------------
Directrix:
The directrix of  is the equation is the equation  . .
Since  , this means that the directrix is , this means that the directrix is 
------------------------------------------------------------
Axis of Symmetry:
In this case, the axis of symmetry is simply the equation of the vertical line through the vertex.
Since  , this means that the axis of symmetry is , this means that the axis of symmetry is 
Visual Check:

Graph of  with the vertex, focus, directrix (green) and axis of symmetry (blue) with the vertex, focus, directrix (green) and axis of symmetry (blue)
|
|
|
| |