Question 193345This question is from textbook
: I have a problem that states to ADD THE PROPER CONSTANT TO EACH BINOMIAL SO THAT THE RESULTING TRINOMIAL IS A PERFECT SQUARE TRINOMIAL. THEN FACTOR EACH TRINOMIAL.
x^2-18x+____
How would you solve this?
any help would be greatly appreciated!!
This question is from textbook
Found 2 solutions by Mathtut, RAY100:
Answer by Mathtut(3670)   (Show Source): (Show Source):
You can put this solution on YOUR website! the constant is always 1/2 of the x terms coefficient squared
:
so in this case the coefficient is -18. divide 18 by 2 and you arrive at -9. The square of -9 equals 81
:
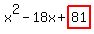 ---> ---> 
Answer by RAY100(1637)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is a secret THEY didn't tell you
This is called completing the square
X^2-18x =#
always divide the coefficient of the second term by 2,,,and them square this
for example,
coefficient is -18,,, -18/2=-9,,,,(-9)^2=81
if we add this to above we get
x^2-18x+81=#+81,,,,,must add to both sides of eqn to keep equal
factoring
(x-9)(x-9)=#+81
(x-9)^2=#+81
do not mean to confuse here,,,by adding =#+81,,,but this is next lesson
,,,,
this comes from the distribution, FOIL, of
(x-9)^2=(x-9)(x-9)= x^2-9x-9x+81=x^2-2(9)x+81=x^2-18x+81
completing the square is just the opposite
|
|
|