|
Question 193197: How do i do question number 77 on 10.3
Write an equation of the line that is tangent to the circle at that point.
77) x2+ y2= 244; (-10, -12)
Please explain the steps..
Found 2 solutions by jim_thompson5910, Alan3354:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find the tangent line, we need the slope of the tangent line. To find that, we first need the first derivative of "y":
 ... Start with the given equation. ... Start with the given equation.
=\frac{d}{dx}(244)) ... Derive both sides with respect to "x" ... Derive both sides with respect to "x"
 ... Derive the left and right sides. Note: remember, y is a function of "x", so use the chain rule. ... Derive the left and right sides. Note: remember, y is a function of "x", so use the chain rule.
 ... Subtract 2x from both sides. ... Subtract 2x from both sides.
 ... Divide both sides by 2y. ... Divide both sides by 2y.
 ... Reduce ... Reduce
So the slope of any tangent line at the point (x,y) (on the circle) is 
Now just plug in the values  and and  to find the tangent slope at (-10,-12): to find the tangent slope at (-10,-12):

 ... Reduce ... Reduce
So the slope of the tangent line is 
Now let's find the equation of the line that has a slope of  and goes through (-10, -12): and goes through (-10, -12):
If you want to find the equation of line with a given a slope of 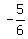 which goes through the point (-10,-12), you can simply use the point-slope formula to find the equation: which goes through the point (-10,-12), you can simply use the point-slope formula to find the equation:
---Point-Slope Formula---
 where where  is the slope, and is the slope, and ) is the given point is the given point
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite 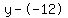 as as 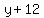
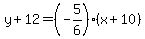 Rewrite Rewrite  as as 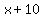
 Distribute Distribute 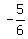
 Multiply Multiply 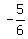 and and  to get to get 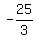
 Subtract 12 from both sides to isolate y Subtract 12 from both sides to isolate y
 Combine like terms Combine like terms 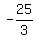 and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the tangent line is 
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Write an equation of the line that is tangent to the circle at that point.
77) x2+ y2= 244; (-10, -12)
Please explain the steps..
----------------
The slope, m, of a circle (and ellipse) at any point is -x/y (if you need to see proof of that, email me via the thank you note)
At (-10,-12), m = -5/6
-----------------
y+12 = -(5/6)*(x+10)
6y+72 = -5x - 50
5x+6y = -122
|
|
|
| |