Question 193178: An object that is projected straight downward with initial velocity of v feet per second is at a height from ground  , where s = initial height in feet, and t = time in seconds. If Bianca is standing on a ledge 46.75 feet above the ground and throws a penny straight down with an initial velocity of 12 feet per second, in how many seconds will it reach the ground? -- I tried as hard as I can to solve this word problem but the answer was not reasonable... please help me, thank you! , where s = initial height in feet, and t = time in seconds. If Bianca is standing on a ledge 46.75 feet above the ground and throws a penny straight down with an initial velocity of 12 feet per second, in how many seconds will it reach the ground? -- I tried as hard as I can to solve this word problem but the answer was not reasonable... please help me, thank you!
Found 2 solutions by nerdybill, josmiceli:
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! An object that is projected straight downward with initial velocity of v feet per second is at a height from ground  , where s = initial height in feet, and t = time in seconds. If Bianca is standing on a ledge 46.75 feet above the ground and throws a penny straight down with an initial velocity of 12 feet per second, in how many seconds will it reach the ground? , where s = initial height in feet, and t = time in seconds. If Bianca is standing on a ledge 46.75 feet above the ground and throws a penny straight down with an initial velocity of 12 feet per second, in how many seconds will it reach the ground?
.

The problem gives you:
s (initial height) as 46.75 feet
v (initial velocity) as 12 feet/sec
.
Since they want to know when it will reach the ground -- h (height) would be 0.
So, set h = 0 and solve for 't':
.


Since we can't factor, use the quadratic equation to solve. Doing so yields:
t={-2.125, 1.375}
Throw out the negative solution -- this leaves:
t = 1.375 seconds
.
Details of quadratic follows:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=3136 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 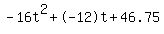 can be factored: can be factored:

Again, the answer is: -2.125, 1.375.
Here's your graph:
 |
Answer by josmiceli(19441)   (Show Source): (Show Source):
|
|
|