Question 192966: You guys are great. Please help . Reduce /simplify the fractions or square root
1. 14/21
2. AB^2C/A^3BC
3.(x-2)(x-3)/2(x-3)
4.2x^2-2x-4/x^2-1
5. Square root of 49
6. Square root of 18
7. 36/64 this question has line on the top and sides of both.
Found 2 solutions by jim_thompson5910, RAY100:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
| Solved by pluggable solver: Reducing Fractions Calculator |
In order to reduce 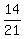 , the numerator and denominator must share a common factor. This common number must evenly divide into both of them without any remainder or decimal. , the numerator and denominator must share a common factor. This common number must evenly divide into both of them without any remainder or decimal.
In order to completely reduce the fraction, you must divide the numerator and the denominator by the greatest common factor (GCF). The GCF of  and and  is is  (note: click here if you need help with finding the GCF). So divide both the numerator and denominator by (note: click here if you need help with finding the GCF). So divide both the numerator and denominator by 
In other words, to reduce the fraction you do this

 Plug in the numerator, denominator, and the GCF Plug in the numerator, denominator, and the GCF
 Now divide 14 by to get 2. This is now the new numerator. Now divide 14 by to get 2. This is now the new numerator.
 Now divide 21 by to get 3. This is now the new denominator. Now divide 21 by to get 3. This is now the new denominator.
So

This means that 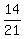 reduces to reduces to 
In other words, 
|
# 2
 Start with the given expression Start with the given expression
 Factor Factor
 Highlight the common terms. Highlight the common terms.
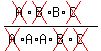 Cancel out the common terms. Cancel out the common terms.
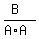 Simplify Simplify
 Multiply Multiply
So  where every variable CANNOT equal 0. where every variable CANNOT equal 0.
# 3
 Start with the given expression Start with the given expression
 Highlight the common terms. Highlight the common terms.
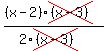 Cancel out the common terms. Cancel out the common terms.
 Simplify Simplify
So  where where 
# 4
 Start with the given expression Start with the given expression
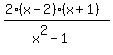 Factor the numerator Factor the numerator
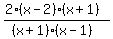 Factor the denominator Factor the denominator
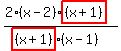 Highlight the common terms. Highlight the common terms.
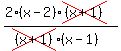 Cancel out the common terms. Cancel out the common terms.
 Simplify Simplify
 Distribute Distribute
So  where where  or or 
# 5
To find,  , let's list the first few perfect squares. To find the perfect squares, just square 0 to get 0, square 1 to get 1, square 2 to get 4, square 3 to get 9, etc... , let's list the first few perfect squares. To find the perfect squares, just square 0 to get 0, square 1 to get 1, square 2 to get 4, square 3 to get 9, etc...
So the first few perfect squares are:
 , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , , 
Notice that  . Remember that the square root "undoes" a square. So . Remember that the square root "undoes" a square. So  or simply or simply 
# 6
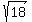 Start with the given expression Start with the given expression
The goal of simplifying expressions with square roots is to factor the radicand into a product of two numbers. One of these two numbers must be a perfect square. When you take the square root of this perfect square, you will get a rational number.
So let's list the factors of 18
Factors:
1, 2, 3, 6, 9, 18
Notice how 9 is the largest perfect square, so lets factor 18 into 9*2
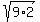 Factor 18 into 9*2 Factor 18 into 9*2
 Break up the square roots using the identity Break up the square roots using the identity 
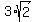 Take the square root of the perfect square 9 to get 3 Take the square root of the perfect square 9 to get 3
So the expression 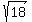 simplifies to simplifies to 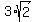
In other words, 
----------------------------
Check:
Notice if we evaluate the square root of 18 with a calculator we get

and if we evaluate 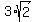 we get we get

This shows that  . So this verifies our answer . So this verifies our answer
# 7
I don't know what you mean here....
Answer by RAY100(1637)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) 14/21 divide num & den by 7 =2/3
2) check if this is right problem
(a b^2c) / (a^3bc
to divide common bases, subtract exponents
taking one variable at a time
a^1/a^3 = a6(1-3) = a^(-2) = 1/(a^2)
b^2/b=b^(2-1)=b^1=b
c^1/c^1=c^(1-1)=c^0=1
recombining
answer = B/A^2
3) check to see if correct problem
((x-2)(x-3))/ (2(x-3))
(x-3)/(x-3)=1
(x-2)/2
4) ( 2x^2-2x-4)/(x^2-1)
factor numerator and denominator
((2)(x-2)(x+1))/((x+1)(x-1))
(x+1)/(x+1)=1
(2(x-2))/(x-1)
5) sqrt49=+/- 7
6) sqrt18=sqrt(9*2)=sqrt9*sqrt2=+/- 3sqrt2
7) (36)/(64) dive num & den by 4 = 9/16
|
|
|