SOLUTION: If 31z5 is a multiple of 9, where z is a digit, what is the value of z?

Algebra ->  Divisibility and Prime Numbers -> SOLUTION: If 31z5 is a multiple of 9, where z is a digit, what is the value of z?      Log On


   

Question 192950: If 31z5 is a multiple of 9, where z is a digit, what is the value of z?
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
If 31z5 is a multiple of 9 (where z is a single digit), then the digits MUST add to a number that is a multiple of 9 (hopefully, they will add to 9 itself).


So the digits must add to 0, 9, 18, 27, 36, 45, 54, 63, 72, etc...


So this gives us the equation:

3%2B1%2Bz%2B5=9k where "k" is an integer (ie whole number)

-----------------------------------------------------

So if k=1 (the smallest possible k value where we get a solution), then...

3%2B1%2Bz%2B5=9

Solve for "z" to get: z%2B9=9 ---> z=0


So when k=1, then z=0 giving the number 3105


So 3105 is divisible by 9. Check: 3105%2F9=345 remainder 0.



-----------------------------------------------------

If k=2, then...

3%2B1%2Bz%2B5=18

Solve for "z" to get: z%2B9=18 ---> z=9


So when k=1, then z=9 giving the number 3195


So 3195 is divisible by 9. Check: 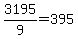3195%2F9=395 remainder 0.




-----------------------------------------------------

If k=3, then...

3%2B1%2Bz%2B5=27

Solve for "z" to get: z%2B9=27 ---> z=18


But since "z" is a single digit, this means that 0%3C=z%3C=9. So ANY value of "k" greater than 2 will give us a "z" value greater than 9. So this means that we're done looking for values of "z".


=========================================================

Answer:

So the two values of "z" are 0 and 9 produce the multiples of 9 3105 and 3195 respectively.