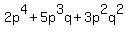 First factor out
First factor out 
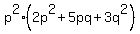 In the parentheses, multiply the first coefficient 2
by the last coefficient 3, getting 6. Write down
all pairs of integer factors whose product is 6.
They are
1*6
2*3
Since the last sign in the parentheses is +, we
add those:
1+6 = 7
2+3 = 5
Since the middle coefficient of
In the parentheses, multiply the first coefficient 2
by the last coefficient 3, getting 6. Write down
all pairs of integer factors whose product is 6.
They are
1*6
2*3
Since the last sign in the parentheses is +, we
add those:
1+6 = 7
2+3 = 5
Since the middle coefficient of 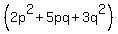 is 5, and since 5 = 2+3 we write 5pq as 2pq+3pq
is 5, and since 5 = 2+3 we write 5pq as 2pq+3pq
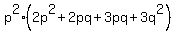 Factor the first two terms in the parentheses by factoring
out
Factor the first two terms in the parentheses by factoring
out 
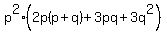 Factor the last two terms in the parentheses by factoring
out
Factor the last two terms in the parentheses by factoring
out 
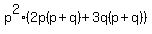 Inside the parentheses take out
Inside the parentheses take out 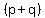
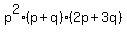 Edwin
Edwin