Question 191261: Please help me factorize and state the roots of the following polynomial. Please, I beg you, I need to know how to to this and would really appreciate whatever help I can get. This was a take home assignment. Thanks.
P(x)=4x^7+28x^6+27x^5-203x^4-591x^3-431x^2+146x+120
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Wow, this is as long as it gets (well I hope so anyway...). Here are two ways to do this:
Method #1:
Use the rational root theorem to find all of the possible roots and test EVERY possible root to see if it is actually a root. Since the degree of the equation is 7, this means that once you find 7 roots, then you don't need to check any more possible roots.
Here's where this method gets really tedious: there are A LOT of possible roots (48 in total)
But, here's how to find them:
Any rational zero can be found through this equation
 where p and q are the factors of the last and first coefficients where p and q are the factors of the last and first coefficients
So let's list the factors of 120 (the last coefficient):

Now let's list the factors of 4 (the first coefficient):

Now let's divide each factor of the last coefficient by each factor of the first coefficient

Now simplify
These are all the distinct rational zeros of the function that could occur

Once you have all of the possible rational roots, either plug them in directly or use synthetic division to determine which ones are actually roots.
Method #2:
Since the first method seems like a lot of busy work (which it is), just use a graphing calculator to find some of the roots, and then use those roots to find other roots (using synthetic division). Eventually, you'll reduce that massive polynomial to a quadratic which you can solve using the quadratic formula.
If you're completely stuck, then repost or email me. By the way, the 7 roots are: 3, -1/2, 1/2, -4, -2, -2+i, -2-i
Also, 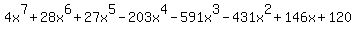 completely factors (over the reals) to completely factors (over the reals) to 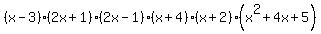
In other words, 
|
|
|