Question 190669: If a vendor charges p dollars each for rugby shirts, then he expects to sell 2000-100p shirts at a tournament.
Find a polynomial R(p) that represents the total revenue
when the shirts are p dollars each.
Find R(5), R(10), and R(20).
So far I have R=(2000-100)P(2000-100^2)
then I'm lost after that.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Remember, the revenue is simply the money that a individual/company has made BEFORE any expenses or taxes are accounted for. So this amount of money is solely determined by the amount of products/services that have been sold.
So basically, the revenue is
Revenue = (Price Per Product) x (Number of Products Sold)
In this case, since "a vendor charges p dollars each for rugby shirts", this means that the price is simply "p" and because "he expects to sell 2000-100p", this means that the number of products sold is 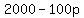
So just multiply the price by the quantity to get

 Distribute Distribute
 Rearrange the terms. Rearrange the terms.
So the polynomial that represents the revenue is 
----------------------------------------------
Find R(5):
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Square Square  to get to get  . .
 Multiply Multiply  and and  to get to get 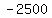 . .
 Multiply Multiply  and and  to get to get 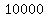 . .
 Combine like terms. Combine like terms.
So this means that if the price is $5 a shirt, then he'll expect to make $7,500
----------------------------------------------
Find R(10):
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Square Square  to get to get  . .
 Multiply Multiply  and and  to get to get 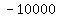 . .
 Multiply Multiply  and and  to get to get 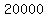 . .
 Combine like terms. Combine like terms.
So this means that if the price is $10 a shirt, then he'll expect to make $10,000
----------------------------------------------
Find R(20):
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Square Square  to get to get  . .
 Multiply Multiply  and and  to get to get 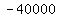 . .
 Multiply Multiply  and and  to get to get 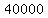 . .
 Combine like terms. Combine like terms.
So if the price is $20 per shirt, then he'll break even (he will neither gain or lose money).
|
|
|