SOLUTION: # 9. Mike invested $7000 for one year. He invested part of it at 8% and the rest at 12%. At the end of the year he earned $764 in interest. How much did he invest at each rate?

Algebra ->  Expressions-with-variables -> SOLUTION: # 9. Mike invested $7000 for one year. He invested part of it at 8% and the rest at 12%. At the end of the year he earned $764 in interest. How much did he invest at each rate?       Log On


   

Question 190617: # 9. Mike invested $7000 for one year. He invested part of it at 8% and the rest at 12%. At the end of the year he earned $764 in interest. How much did he invest at each rate?

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
# 9
Q: Mike invested $7000 for one year. He invested part of it at 8% and the rest at 12%. At the end of the year he earned $764 in interest. How much did he invest at each rate?

A:

Let
x = amount of money Mike invests at 8%
y = amount of money Mike invests at 12%

Since "Mike invested $7000 for one year.", this means that x%2By=7000


Also, because "He invested part of it at 8% and the rest at 12%. At the end of the year he earned $764 in interest.", this translates to 0.08x%2B0.12y=764. Multiplying every term by 100 gets us 8x%2B12y=76400


So we have the system of equations:


system%28x%2By=7000%2C8x%2B12y=76400%29


Let's solve this system by substitution



Now in order to solve this system by using substitution, we need to solve (or isolate) one variable. I'm going to solve for y.




So let's isolate y in the first equation

x%2By=7000 Start with the first equation


y=7000-x Subtract x from both sides


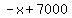y=-x%2B7000 Rearrange the equation


---------------------

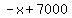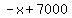
Since y=-x%2B7000, we can now replace each y in the second equation with -x%2B7000 to solve for x



8x%2B12%2Ahighlight%28%28-x%2B7000%29%29=76400 Plug in y=-x%2B7000 into the second equation. In other words, replace each y with -x%2B7000. Notice we've eliminated the y variables. So we now have a simple equation with one unknown.



8x%2B%2812%29%28-1%29x%2B%2812%29%287000%29=76400 Distribute 12 to -x%2B7000


8x-12x%2B84000=76400 Multiply


-4x%2B84000=76400 Combine like terms on the left side


-4x=76400-84000Subtract 84000 from both sides


-4x=-7600 Combine like terms on the right side


x=%28-7600%29%2F%28-4%29 Divide both sides by -4 to isolate x



x=1900 Divide


So this means that Mike invested $1,900 at 8%


-----------------------------

Since we know that x=1900 we can plug it into the equation y=-x%2B7000 (remember we previously solved for y in the first equation).



y=-x%2B7000 Start with the equation where y was previously isolated.


y=-%281900%29%2B7000 Plug in x=1900


y=5100 Combine like terms


So Mike invested $5,100 at 12%

===============================================
Answer:

So Mike invested $1,900 at 8% and $5,100 at 12%