Question 190609: # 1. Use inductive reasoning to determine the next three numbers in the pattern: 1, 1/3, 1/9, 1/27, ...
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
Q: Use inductive reasoning to determine the next three numbers in the pattern: 1, 1/3, 1/9, 1/27, ...
A:
From the first term 1 to the second term  , notice how the second term is just the first term divided by 3. So let's see if this holds from the second term to the third term. , notice how the second term is just the first term divided by 3. So let's see if this holds from the second term to the third term.
If we divide  by by  , we get: , we get: 
So this shows that if we divide  by by  , we get , we get 
--------------------------------
Now let's divide  , by , by  to get: to get:

So dividing  by by  gets us gets us 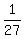
So using inductive reasoning, we would conjecture that this pattern continues indefinitely.
So this means that we can find the next three terms by dividing each previous term by 3.
So divide 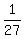 by 3 to get by 3 to get

So the next term is 
----------
Now divide  by 3 to get by 3 to get

So the next term is 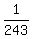
----------
So divide 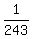 by 3 to get by 3 to get

So the next term is 
======================
Answer:
So the next three terms of the sequence are  , , 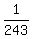 , and , and 
|
|
|