Question 189987: Please help I have tried and cant come up with the solution.
. Find the equation, in standard form, of the line perpendicular to 2x - 3y = -5 and passing through (3, -2). Write the equation in standard form, with all integer coefficients.
2x-3y= -5 and write in standard form which is Ax+By=C now to break it down.
A=2x,B=3y,C=-5
2x+(-3)y=-5
4. Solve the system of equations using the substitution method.
If the answer is a unique solution, present it as an ordered pair: (x, y). If not, specify whether the answer is "no solution" or "infinitely many solutions" and state how you arrived at that conclusion.
3x + y = 2
2x - y = 3
5. Solve the system of equations using the addition (elimination) method.
If the answer is a unique solution, present it as an ordered pair: (x, y). If not, specify whether the answer is "no solution" or "infinitely many solutions" and state how you arrived at that conclusion.
3x - 11y = 9
-9x + 33y = -27
6. Solve the system of equations using the addition (elimination) method.
If the answer is a unique solution, present it as an ordered pair: (x, y). If not, specify whether the answer is "no solution" or "infinitely many solutions" and state how you arrived at that conclusion.
4x + 10y = 2
3x + 5y = 5
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please help I have tried and cant come up with the solution.
. Find the equation, in standard form, of the line perpendicular to 2x - 3y = -5 and passing through (3, -2). Write the equation in standard form, with all integer coefficients.
:
First we have to find the slopes, we need it in the slope intercept form for this:
2x - 3y = -5; this is the standard form
-3y = -2x - 5
Get rid of all those negatives, multiply eq by -1
3y = 2x + 5
Divide by 3 to get y
y =  x + x + 
The slope of this equation (m1) is 
:
Find the slope (m2) of the perpendicular line: m1*m2 = -1
 *m2 = -1 *m2 = -1
m2 = -1 * 
m2 = 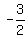 is the slope of the perpendicular line is the slope of the perpendicular line
:
It passes thru 3,-2 write the equation using the point/slope form y-y1 = m(x-x1)
y - (-2) = 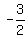 (x - 3) (x - 3)
y + 2 = 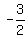 x + x + 
y = 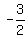 x + x +  - 2 - 2
y = 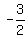 x + x +  - - 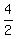
y = 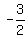 x + x +  is the equation is the equation
To put it in the standard form, multiply equation by 2
2y = -3x + 5
+3x + 2y = 5 is the standard form of the perpendicular line
:
Check it using the given coordinates 3, -2
3(3) + 2(-2) = 5
9 - 4 = 5, confirms our equation
:
:
4. Solve the system of equations using the substitution method.
If the answer is a unique solution, present it as an ordered pair: (x, y). If not, specify whether the answer is "no solution" or "infinitely many solutions" and state how you arrived at that conclusion.
3x + y = 2
2x - y = 3
:
Use the 1st equation for substitution
y = -3x + 2
Substitute (-3x+2) for y in the 2nd equation
2x - (-3x+2) = 3
2x + 3x - 2 = 3; minus a minus is a plus
5x = 3 + 1
5x = 5
x = 1
:
Substitute 1 for x in the 1st equation find y
3(1) + y = 2
3 + y = 2
y = 2 - 3
y = -1
:
Check solutions in the 2nd equation (2x - y = 3)
2(1) - (-1) = 3
2 + 1 = 3; confirms our solutions, ordered pair: 1, -1
:
:
5. Solve the system of equations using the addition (elimination) method.
If the answer is a unique solution, present it as an ordered pair: (x, y). If not, specify whether the answer is "no solution" or "infinitely many solutions" and state how you arrived at that conclusion.
3x - 11y = 9
-9x + 33y = -27
multiply the 1st equation by 3, add to the 2nd equation
+9x - 33y = 27
-9x + 33y = -27
-------------------adding eliminates everything, there is no solution
:
:
6. Solve the system of equations using the addition (elimination) method.
If the answer is a unique solution, present it as an ordered pair: (x, y). If not, specify whether the answer is "no solution" or "infinitely many solutions" and state how you arrived at that conclusion.
4x + 10y = 2
3x + 5y = 5
Multiply the 2nd equation by -2 add to the 1st equation
+4x + 10y = 2
-6x - 10y = -10
------------------adding eliminates y, find x
-2x = -8
x = 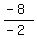
x = +4
:
Find y using the 1st equation
4(4) + 10y = 2
16 + 10y = 2
10y = 2 - 16
10y = -14
y = 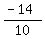
y = -1.4
:
Check solution in the 2nd equation:
3(4) + 5(-1.4) = 5
12 - 7 = 5; confirms our solutions, ordered pair: 4, -1.4
|
|
|