Question 189534: sin theta= 12/13, 3pi/2
cos-1/4,csc theta>0, find sin 2theta,cos 2theta, tan 2theta
Found 2 solutions by Edwin McCravy, feliz1965:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I can do your 2nd problem but not the 1st, for you've
made a mistake in copying the first problem. Here's why:
sinq = 12/13, 3p/2 < q < 2p. Find sin2q, cos2q, tan2q?
3p/2 < q < 2p
tells us that q is in quadrant IV.
But the sine is negative in quadrant IV, yet you have
sinq = 12/13, which is a positive number.
That cannot be.
-----------------
Here's your 2nd problem:
cosq = -1/4,cscq > 0, find sin2q,cos2q, tan2q
This tells us that q is in quadrant II,
because that is the only quadrant in which the cosine is negative and
the cosecant is positive.
So we draw an angle in Quadrant II to represent angle q
 Next we draw a perpendicular to the x axis. Since the cosine
is
Next we draw a perpendicular to the x axis. Since the cosine
is  , we make the x value -1, which is the numerator of , we make the x value -1, which is the numerator of
 and make the hypotenuse or the r equal to the the
denominator of and make the hypotenuse or the r equal to the the
denominator of  which is 4: which is 4:
 Next we calculate the value of y by the Pythagorean
theorem equation
Next we calculate the value of y by the Pythagorean
theorem equation




 So we label the y-value with that
So we label the y-value with that
 Now we can find sin2q using the
identity:
sin2q = 2sinqcosq
because we now know that sinq =
Now we can find sin2q using the
identity:
sin2q = 2sinqcosq
because we now know that sinq =  = = 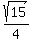 , and cosq = , and cosq =  = =  .
sin2q = 2sinqcosq = .
sin2q = 2sinqcosq =  Next we find cos2q using any one of
these three identities:
cos2q = cos2q - sin2q
cos2q = 2cos2q - 1
cos2q = 1 - 2sin2q.
I'll choose the second one, although any one will give you the
same answer:
cos2q = 2cos2q - 1
cos2q = 2
Next we find cos2q using any one of
these three identities:
cos2q = cos2q - sin2q
cos2q = 2cos2q - 1
cos2q = 1 - 2sin2q.
I'll choose the second one, although any one will give you the
same answer:
cos2q = 2cos2q - 1
cos2q = 2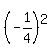 - 1
cos2q = 2 - 1
cos2q = 2 - 1
cos2q = - 1
cos2q = 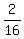 - 1
cos2q = - 1
cos2q =  - 1
cos2q = - 1
cos2q =  Finally we can find tan2q from
the identity
tan2q = sin2q/cos2q
tan2q =
Finally we can find tan2q from
the identity
tan2q = sin2q/cos2q
tan2q =  Edwin
Edwin
Answer by feliz1965(151)   (Show Source): (Show Source):
You can put this solution on YOUR website! sin theta= 12/13, 3pi/2
I will use t for theta.
So, let t = theta for short.
sin(t)= 12/13
We make a right triangle knowing that sine equals opposite side divided by hypotenuse.
We need to find one of the legs of this right triangle.
Let x = the missing leg.
x^2 + (12)^2 = (13)^2
x^2 + 144 = 169
x^2 = 169 - 144
x^2 = 25
x = 5
The missing leg is 5.
=====================
We now need to know what sin2(t), cos2(t) and tan2(t) stand for.
cosine = adjacent side of right triangle divided by hypotenuse.
tangent = opposite side of right triangle divided by the adjacent side of the right triangle.
sin2(t) = 2sin(t) times cos(t)
I will do this one only. I then will give you the information you need to solve the other two trig expressions.
sin2(t) = 2sin(t) times cos(t)
Before I can go on, I need to know what cos(t) stands for. To do so, I go back to the right triangle knowing that cosine = adjacent side/hypotenuse.
sin(t) was given to be 12/13.
If cosine = adjacent side/hypotenuse, then cos(t) = 5/13.
I now have everything to solve for sin2(t).
sin2(t) = 2(12/13) times 5/13
sin2(t) = 120/169
===========================================
You will need to find the rest.
Here is the data you need:
tangent = 12/5
cos2(t) = cos^2 (t) - sin^2 (t)
tan2(t) = [2tan(t)]/[1 - tan^2 (t)]
I gave you everything you need.
All you have to do and plug and chug.
Can you take it from here?
|
|
|