Question 189239This question is from textbook McDougal Littel Algebra 1
: This is an Area Problem.
The directions say:Find the dimensions of the rectangle or triangle that has the given area.
number 44, the area is 34 square meters. the length of the rectangle is (X+11)m and the width is (X-4). I cannot figure out how to start the problem.
THIS IS URGENT SO CAN YOU PLEASE GET BACK TO ME BEFORE TONIGHT.
This question is from textbook McDougal Littel Algebra 1
Found 2 solutions by jim_thompson5910, jonvaliente:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Because "the area is 34 square meters", this tells us that 
Since the "length of the rectangle is (X+11)m", this means that 
Also, since "the width is (X-4)", this means that 
 Start with the area of a rectangle formula Start with the area of a rectangle formula
 Plug in Plug in  , ,  and and 
 FOIL FOIL
 Subtract 34 from both sides. Subtract 34 from both sides.
 Combine like terms. Combine like terms.
Notice we have a quadratic equation in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for x
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get 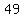 . .
 Multiply Multiply 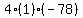 to get to get 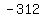
 Rewrite Rewrite 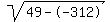 as as 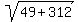
 Add Add 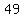 to to 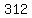 to get to get 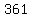
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of 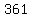 to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the possible answers are  or or 
However, if we plug in  into either into either  or or  , we get , we get
 ... ... 
Since a negative length or width doesn't make any sense, we must discard this possible solution
So the only solution for "x" is 
This means that the length and width are:
Length: 
Width: 
So the length is 17 meters and the width is 2 meters.
Answer by jonvaliente(64)   (Show Source): (Show Source):
|
|
|