|
Question 189027This question is from textbook applied college algebra
: find the equation of the line that contains the point (-1, -3) and is perpendicular to the graph of 3x-5y=2
This question is from textbook applied college algebra
Found 2 solutions by jojo14344, Alan3354:
Answer by jojo14344(1513)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given line 3x-5y=2 in Slope-Intercept Form --> ; ;
 , divide by "5" both terms (left & right): , divide by "5" both terms (left & right):


Above line Eqn has a 
The Line passing thru point (-1,-3) perpendicular to 3x-5y=2 has a 
Then thru point (-1,-3) via Slope-Intercept Form:
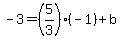
 ---> --->  , Y-Intercept , Y-Intercept
Let fy=0 ----> 
 ----> ----> 
 , X-Intercept , X-Intercept
Therefore, Eqn of the Line is y=(5/3)x-4/3
In Standard Form and removing fractions:
 , multiply whole eqn by 3: , multiply whole eqn by 3:
 , Answer , Answer
We'll see graph:
 --------> perpendicular to --------> perpendicular to , GREEN, 3x-5y=2 , GREEN, 3x-5y=2
Thank you,
Jojo
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the equation of the line that contains the point (-1, -3) and is perpendicular to the graph of 3x-5y=2
-------------------
Step 1, find the slope, m, of the line.
To do that, put the eqn in the slope-intercept form, which means solve for y.
3x-5y=2 --> y = (3/5)x - 2/5
In this form, it's y = mx + b, where m is the slope and b in the y-intercept.
-------------------
Lines parallel to this line have the same slope. The slope of lines perpendicular have a slope that's the negative inverse, m = -5/3
Step 2:
Use y-y1 = m*(x-x1) where (x1,y1) is the point (-1,-3)
y+3 = (-5/3)*(x+1)
y = (-5/3)x - 14/3 (slope-intercept form)
5x + 3y = -14 (standard form)
|
|
|
| |