SOLUTION: Length of a Line Segment 13. A line segment has endpoints K(-2, 7) and L(4, -2). a) Find the coordinates of the midpoint of this line segment. b) Use the length formula to veri

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: Length of a Line Segment 13. A line segment has endpoints K(-2, 7) and L(4, -2). a) Find the coordinates of the midpoint of this line segment. b) Use the length formula to veri      Log On


   

Question 188710: Length of a Line Segment
13. A line segment has endpoints K(-2, 7) and L(4, -2).
a) Find the coordinates of the midpoint of this line segment.
b) Use the length formula to verify your answer to part a).
Thank you very much!!!!
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
a)



To find the midpoint, first we need to find the individual coordinates of the midpoint.


X-Coordinate of the Midpoint:




To find the x-coordinate of the midpoint, simply average the two x-coordinates of the given points by adding them up and dividing that result by 2 like this:


x%5Bmid%5D=%28-2%2B4%29%2F2=2%2F2=1


So the x-coordinate of the midpoint is x=1


-----------------------------------------------------


Y-Coordinate of the Midpoint:




To find the y-coordinate of the midpoint, simply average the two y-coordinates of the given points by adding them up and dividing that result by 2 like this:


y%5Bmid%5D=%287%2B-2%29%2F2=5%2F2


So the y-coordinate of the midpoint is y=5%2F2


So the midpoint between the points and is



---------------------------------------------------------------------

b)


The midpoint of a line segment is equidistant from the endpoints of the segment that it lies on. In other words, the distance from one endpoint to the midpoint is equal to the distance from the other endpoint to the midpoint



So all that you have to do is show that the two distances are equal

part 1)

Let's find the distance from (the first endpoint) to (the midpoint)




d=sqrt%28%28x%5B1%5D-x%5B2%5D%29%5E2%2B%28y%5B1%5D-y%5B2%5D%29%5E2%29 Start with the distance formula.


d=sqrt%28%28-2-1%29%5E2%2B%287-5%2F2%29%5E2%29 Plug in x%5B1%5D=-2, x%5B2%5D=1, y%5B1%5D=7, and y%5B2%5D=5%2F2.


d=sqrt%28%28-3%29%5E2%2B%287-5%2F2%29%5E2%29 Subtract 1 from -2 to get -3.


d=sqrt%28%28-3%29%5E2%2B%289%2F2%29%5E2%29 Subtract 5%2F2 from 7 to get 9%2F2.


d=sqrt%289%2B%289%2F2%29%5E2%29 Square -3 to get 9.


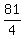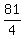d=sqrt%289%2B81%2F4%29 Square 9%2F2 to get 81%2F4.


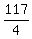d=sqrt%28117%2F4%29 Add 9 to 81%2F4 to get 117%2F4.


d=%283%2Asqrt%2813%29%29%2F2 Simplify


--------------------------------------------------------------

part 2)


Now let's find the distance from (the midpoint) to (the second endpoint)



d=sqrt%28%28x%5B1%5D-x%5B2%5D%29%5E2%2B%28y%5B1%5D-y%5B2%5D%29%5E2%29 Start with the distance formula.


d=sqrt%28%281-4%29%5E2%2B%285%2F2--2%29%5E2%29 Plug in x%5B1%5D=1, x%5B2%5D=4, y%5B1%5D=5%2F2, and y%5B2%5D=-2.


d=sqrt%28%28-3%29%5E2%2B%285%2F2--2%29%5E2%29 Subtract 4 from 1 to get -3.


d=sqrt%28%28-3%29%5E2%2B%289%2F2%29%5E2%29 Subtract -2 from 5%2F2 to get 9%2F2.


d=sqrt%289%2B%289%2F2%29%5E2%29 Square -3 to get 9.


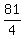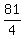d=sqrt%289%2B81%2F4%29 Square 9%2F2 to get 81%2F4.


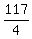d=sqrt%28117%2F4%29 Add 9 to 81%2F4 to get 117%2F4.


d=%283%2Asqrt%2813%29%29%2F2 Simplify


Since the two distances are equal, this shows us that the two lengths are equal.


So this proves that the midpoint between the points and is