|
Question 188303: The profit on a watch is given by P = x2 – 13x – 80 and where x is the number of watches sold per day. How many watches were sold on a day when there was a $50 loss?
Found 2 solutions by jojo14344, Mathtut:
Answer by jojo14344(1513)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let known P=Y=Profit or Losses
Solving for "x" for number of watches. More importantly to see the X-Intercepts.
Given:
By Quadratic, where
Discriminant: b^2-4ac= -13^2 - 4(1)(-80)=169+320=489
Then,



X-Intercepts = > (17.55,0) & (-4.55,0)
For Y-Intercept:
Let fx=0 ----> 
Y-Intercept = > (0,-80)
We now get the vertex thru Vertex-Form, 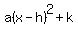 , where , where
Going back to our eqn:
 , complete the square, by taking "Half" of the middle constant then "squared": , complete the square, by taking "Half" of the middle constant then "squared":
In our eqn, the middle constant is 13, taking half of it =  , then squared it= , then squared it=  . We "add" and also "subtract" to the eqn: . We "add" and also "subtract" to the eqn:

 --->follows --->follows 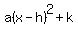
In our eqn, we have vertex, h=x=6.5 & k=y=-122.25
We see graph,

The Y axis, is where the Profit or Losses.
So if you have a loss of $50, that equals to -50 on the Y axis.
Make a straigth line from -50 on the Y axis to the right until it touches the curve. As it touched the curve, extend the line downwards until it touches the X axis.
This will show the number of watches for the loss sale of $50.00.
 ----> 15 watches sold for a loss of $50.00 ----> 15 watches sold for a loss of $50.00
Let's check,
Go back our Eqn, & substitute x=15:

 , Loss , Loss
Thank you,
Jojo
Answer by Mathtut(3670)   (Show Source): (Show Source):
|
|
|
| |