Your 8 in the top should have been 40.
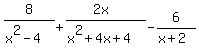Factor the first two denominators:
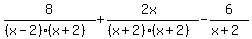Now let's create the LCD:
appears 1 time in the first denominator,
0 time in the second denominator and 0 times in the
third denominator. That's at most 1 time, so it
has to be included in the LCD 1 time
appears 1 time in the first denominator,
2 times in the second denominator and 1 times in the
third denominator. That's at most 2 times, so it
has to be included in the LCD 2 times
So the LCD contains 1 time and
2 times. So:
LCD =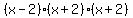 
Each of the three terms must be rewritten so that each
fraction has the LCD as its denominator.
The first fraction is
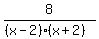Its denominator needs another factor to become
the LCD, so we multiply its numerator and denominator by
The second fraction is
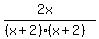Its denominator needs an factor to become
the LCD, so we multiply its numerator and denominator by
The third fraction is
Its denominator needs another factor and
another factor to become the LCD, so we
multiply its numerator and denominator by
So
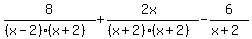now becomes:
Multiply out the numerators only:
The last numerator still needs one more step to be multiplied
out:
Now we combine all the numerators over the LCD:
Remove all the parentheses on the top, but not on the bottom.
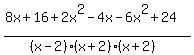Combine all like terms on the top:
If you like you may arrange the top in descending powers of x:
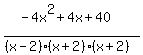and you see that there is a 40 where you had 8. If
you like you can factor -4 out of the top, and as you
did, write 
instead of 
in
the bottom:
But we find that the quadratic in the parenthese does not
factor, so that's as far as we can go.
Edwin
