Question 186740: When an arrow is shot in the air, the height of the arrow h(t),at time t, t>or equal to 0, is determined by the equation h(t)= -4tsquared +16t+1.For which interval of time is the height of the arrow greater than or equal to 11 meters?
I figured out the vertex (2,17) and roots are in decimals-.0615528128 and 4.061552813. I believe the 4.061552813 is how long it takes to go up and down, reaching 17 meters going up, but I don't know how long for 11 meters. I missed on how to do this I was sick all week and have no one to explain it to me. Please help me. Chantal Laroche
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! When an arrow is shot in the air, the height of the arrow h(t), at time t,
t>or equal to 0, is determined by the equation h(t)= -4tsquared + 16t + 1.
For which interval of time is the height of the arrow greater than or equal to 11 meters
:
h(t) = -4t^2 + 16t + 1, where t = time in seconds, and h = height at t time.
:
There are three parts to the equation:
-4t^2 is the effect of gravity (usually it's 4.9t^2)
16t is the upward velocity of the arrow
1 is the height above ground (0) that the arrow is launched
:
If you plot this equation, it would look like this:
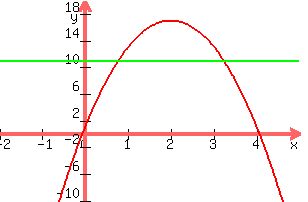
where height is on the y axis and time in sec on the x axis
You can see the vertex is 2,17 as you stated
the green line is at 11 meters
:
To calculate the time (t) that the arrow is at 11 meters; h(t) = 11
-4t^2 + 16t + 1 = 11
:
-4t^2 + 16t + 1 - 11 = 0
:
-4t^2 + 16t - 10 = 0
Use the quadratic formula: a=-4, b=16, c=-10
two solutions
t = .775 sec on the way up
and
t = 3.225 sec on the way down
therefore the arrow is => 11m between .775 sec to 3.225 sec or for 3.225-.775 = 2.45 sec
:
Did this help you understand what's going on here?
|
|
|