1. Is it in rref?
Yes because: going left to right, the VERY FIRST non-zero element
in each row which isn't all zeros has these properties:
A. It is a 1.
B. It has no elements directly above it or below it other than zeros.
C. It is farther to the right than any first non-zero element which
may be above it.
D. If any row has only zeros then it is at the bottom.
2. If it is in rref, what is the solution set?
There is no solution because, as you have discovered,
the bottom row translates to the following equation,
where the 5th variable is 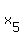
 which has no solution, since no matter what value you
substitute for
which has no solution, since no matter what value you
substitute for 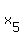 the left side will always be
0 and the right side is 1, and zero can never equal 1.
So the solution set is the empty set which is either
written
the left side will always be
0 and the right side is 1, and zero can never equal 1.
So the solution set is the empty set which is either
written 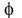 or
or 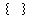
3. If it is not in rref, why?
But it is in rref, which means row reduced echelon form!
Edwin