|
Question 186733: Ok, so I am given 4 matrices and 2 operations to perform (if possible). I don't think the operations can be performed, but would like to verify that that's true.
Here are the 4 matrices:
A =
[2 -1 3]
[0 4 -2]
B =
[-3 1]
[ 2 5]
C =
[-1 0 2]
[ 4 -3 1]
[-2 3 5]
D =
[3 -2]
[0 -1]
[1 2]
Here are the 2 operations:
1. (B^5)A + D (I think the addition of matrices requires identical
dimensions & here we have a 2x2 added to a 3x2)
2. (3)BA + (4)AC (I think the multiplication of matrices requires the
number of rows in the first matrix to match the number
of columns in the second. Here we have B as a 2x2 and
A as a 2x3; then, A as a 2x3 and C as a 3x3)
Thanks for taking a look, I appreciate your assistance.
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website! Ok, so I am given 4 matrices and 2 operations to perform (if possible). I don't think the operations can be performed, but would like to verify that that's true.
Here are the 4 matrices:
A =
[2 -1 3]
[0 4 -2]
B =
[-3 1]
[ 2 5]
C =
[-1 0 2]
[ 4 -3 1]
[-2 3 5]
D =
[3 -2]
[0 -1]
[1 2]
Here are the 2 operations:
1. (B^5)A + D (I think the addition of matrices requires identical
dimensions & here we have a 2x2 added to a 3x2)
2. (3)BA + (4)AC (I think the multiplication of matrices requires the
number of rows in the first matrix to match the number
of columns in the second. Here we have B as a 2x2 and
A as a 2x3; then, A as a 2x3 and C as a 3x3)
Thanks for taking a look, I appreciate your assistance.
The rules are
1. For adding. We can only add a pxq matrix to another pxq matrix
and when we do, we end up with another pxq matrix.
2. For multiplying. We can only multiply a pxq matrix times a qxr
matrix and end up with a pxr matrix.
A is a 2x3 matrix
B is a 2x2 matrix
C is a 3x3 matrix
D is a 3x2 matrix
For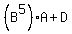 
The first factor in the first term is:
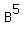That's a 2x2 times a 2x2 times a 2x2 times a 2x2 times a 2x2.
So we end up with another 2x2.
Now the whole first term is:
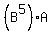So here we are multiplying a 2x2 times A, which is a 2x3.
This can be multiplied and we will get a 2x3.
Now we must add this to D, which is a 3x2. Uh oh!!
We can't add these, so that's undefined. You are right.
------
But I think you're wrong about the second one.
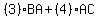The constants (3) and (4) in front do not affect the dimensions.
So we can ignore them to find out if this is defined and, if so,
what kind of matrix we will end up with.
The first term involves chiefly BA. That's a 2x2 times a 2x3.
When that is multiplied, we will get a 2x3.
The second term involves chiefly AC. That's a 2x3 times a 3x3.
When that is multiplied, we will get a 2x3.
So we can add these because they have the same dimensions, and
we will end up with another 2x3 matrix.
The answer to the second problem is this 2x3 matrix
[-66 69 39]
[ 92 -18 -36]
If you have trouble getting this answer, you may email me.
AnlytcPhil@aol.com and I'll help you get it.
Edwin
|
|
|
| |
