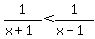 Get 0 on the right
Get 0 on the right
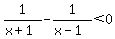 Get LCD of
Get LCD of 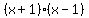
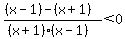
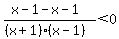
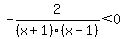 Critical values are gotten by setting
numerators and denominators = 0 and solving.
We can't set the numerator = 0 since it's -2
We set the denominator = 0
Critical values are gotten by setting
numerators and denominators = 0 and solving.
We can't set the numerator = 0 since it's -2
We set the denominator = 0

 and
and  Now we make a number line and mark those critical values
-----------o---------o-----------
-3 -2 -1 0 1 2 3
Now we choose any value to the left of -1, say -2
Substitute it into
Now we make a number line and mark those critical values
-----------o---------o-----------
-3 -2 -1 0 1 2 3
Now we choose any value to the left of -1, say -2
Substitute it into
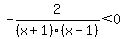
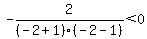

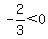 That is true so we shade the part of
the number line to the left of -1:
<===========o---------o-----------
-3 -2 -1 0 1 2 3
Next we choose any value between -1 and 1,
say, 0 and substitute it into
That is true so we shade the part of
the number line to the left of -1:
<===========o---------o-----------
-3 -2 -1 0 1 2 3
Next we choose any value between -1 and 1,
say, 0 and substitute it into
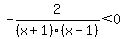
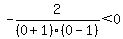
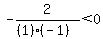
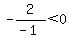
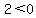 That is false so we do not shade the part of
the number line between -1 and 1, so we still
have:
<===========o---------o-----------
-3 -2 -1 0 1 2 3
Next we choose any value to the right of 1, say 2
Substitute it into
That is false so we do not shade the part of
the number line between -1 and 1, so we still
have:
<===========o---------o-----------
-3 -2 -1 0 1 2 3
Next we choose any value to the right of 1, say 2
Substitute it into
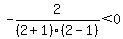
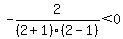
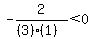
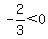 That is true so we shade the part of
the number line to the right of 1:
<===========o---------o==========>
-3 -2 -1 0 1 2 3
The critical values do not satisfy the inequality
because they cause 0's in the denominator, so
we leave them open.
Now we translate this graph into interval notation:
That is true so we shade the part of
the number line to the right of 1:
<===========o---------o==========>
-3 -2 -1 0 1 2 3
The critical values do not satisfy the inequality
because they cause 0's in the denominator, so
we leave them open.
Now we translate this graph into interval notation:
 Edwin
Edwin