Question 184529: I'm can't figure out how to create a quadratic equation out of the vertex and a point that it must pass through. All i've managed so far is some trial and error and come up with this.
y=2(x+2)²+4
From the vertex of (-2,4) and passing through (-1,8).
I have been fiddling around with it and have two ideas how to proceed.
I could change (x+2) to something else to move it along the x axis or change the first part of it to change the fatness or whichever you want to call it of the parabola. Regardless i figure there is a better way to do it other then trial and error, if it has been answered before i'm sorry I didn't see it. I'm self taught and this is the first time I really have had any problem.
-Thanks
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Remember, the general vertex form of an equation is  where "a" is the stretch/compression factor and (h,k) is the vertex. We know what the vertex is, but we don't know the value of "a". So the goal is to find "a". where "a" is the stretch/compression factor and (h,k) is the vertex. We know what the vertex is, but we don't know the value of "a". So the goal is to find "a".
Since the vertex is (-2,4), this tells us that  and and  . .
 Start with the vertex form of the equation Start with the vertex form of the equation
 Plug in Plug in  and and 
 Rewrite Rewrite 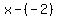 as as 
Now because we want the parabola to pass through the point (-1,8), this means that when  , ,  . So we can plug in . So we can plug in  and and 
 Plug in Plug in  and and  . We finally have an equation with one unknown variable . We finally have an equation with one unknown variable
 Subtract 4 from both sides. Subtract 4 from both sides.
 Combine like terms. Combine like terms.
 Square 1 to get 1 Square 1 to get 1
 Multiply Multiply
So the value of "a" is 
========================================
Answer:
This means that the equation with a vertex of (-2,4) that passes through (-1,8) is 
Here's the graph to visually verify the answer
 Graph of Graph of  with a vertex of (-2,4) that passes through the point (-1,8) with a vertex of (-2,4) that passes through the point (-1,8)
|
|
|