Question 184468: Question 1:
A work word problem
If Adam and Beth would paint the room together, they would need 5 hours. If Adam and Cindy would paint it together, they would need only 4 hours. If Beth and Cindy would paint it together, they would need only 3 hours. How long do they need if all three work together?
Generalize this kind of problem for 4 persons, and solve this as well.
Question 2:
Mixture problem II
You have two large 2 liter container and a small cup of unknown volume. At the beginning you have 1.2 liter of acid solution of unknown concentration in the left container, and 0.9 liter pure acid in the right one. We take one cup of solution from the left container and putting it into the right one. After that we take one cup of the resulting solution from the right container and put into the left container. Finally we again put one cup solution from the left container into the right one. At the end, we have 50% acid solution in the left container and 80% acid solution in the right one. How large is the cup, and what was the initial acid concentration in the left container?
Question 3:
A Cinema Word Problem
In a cinema, the price is 12 SF per person. Students however do only pay 9 SF, and children pay only 1 SF each. If the total amount paid by 41 persons is 400 SF, how many of them were students and how many children?
Solve this problem, discuss the method, and explain wether or not your method can be applied to the general problem where the prices are a, b, c, and the total amount paid by the n persons is m. How does the choice of a, b, c, n, m affect the number of solutions?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A work word problem
If Adam and Beth would paint the room together, they would need 5 hours. If Adam and Cindy would paint it together, they would need only 4 hours. If Beth and Cindy would paint it together, they would need only 3 hours. How long do they need if all three work together?
:
I actually got this one but the process is so lengthy, I am trying to simplify it.
:
Generalize this kind of problem for 4 persons, and solve this as well.
Question 2: can't do this one
;
:
Mixture problem II
You have two large 2 liter container and a small cup of unknown volume. At the beginning you have 1.2 liter of acid solution of unknown concentration in the left container, and 0.9 liter pure acid in the right one. We take one cup of solution from the left container and putting it into the right one. After that we take one cup of the resulting solution from the right container and put into the left container. Finally we again put one cup solution from the left container into the right one. At the end, we have 50% acid solution in the left container and 80% acid solution in the right one. How large is the cup, and what was the initial acid concentration in the left container?
:
A real toughie here, still mulling this one over
:
:
Question 3:
:
A Cinema Word Problem
In a cinema, the price is 12 SF per person. Students however do only pay 9 SF, and children pay only 1 SF each. If the total amount paid by 41 persons is 400 SF, how many of them were students and how many children?
Solve this problem, discuss the method, and explain wether or not your method can be applied to the general problem where the prices are a, b, c, and the total amount paid by the n persons is m. How does the choice of a, b, c, n, m affect the number of solutions?
:
Let a = no. of adults, s = no. of students; c = no. of children
:
Two equations
a + s + c = 41
12a + 9s + 1c = 400
:
They're not asking for the no. of adults, so mult the 1st equation by 12
eliminate a
12a + 12s + 12c = 492
12a + 9s + 1c = 400
------------------------subtraction eliminates a
3s + 11c = 92
3s = 92 - 11s
s = 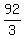 - - 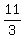 c c
There can't many children so try c=1
s = 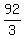 - - 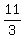
s = 
s = 27 students
then
a = 41 - 28 = 13 adults
:
Check
12(13) + 9(27) + 1 =
156 + 243 + 1 = 400
:
I see there are two more solutions, where c = 4 and c = 7
|
|
|