Question 18327: Greetings everyone!
I could really use some help from one of the wise Math wizards out there! Could someone please help me solve this word problem? I am stumped:
If a baseball is projected upward from ground level with an initial velocity of 64 feet per second, then its height is a function of time, given by s(t) = -16t^2 + 64t. Graph this function for "0" less than or equal to "t" less than or equal to 4. What is the maximum height reached by the ball? This one's a doozie!
Thanks to all.
Answer by xcentaur(357)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If a baseball is projected upward from ground level with an initial velocity of 64 feet per second, then its height is a function of time, given by

Graph this function for (0<=t<=4).
What is the maximum height reached by the ball?
If the ball is thrown upward with some initial velocity,when it reaches its maximum height it will have final velocity equal to zero.
After that it will come down due to gravity.
Now we assign:
initial velocity (u) = 64 feet/s
final velocity (v) = 0 feet/s
If you have done this portion of study of moving objects in school,then read the following:
Using physics we can get:
[v^2=u^2+2aS]
where a=acceleration due to gravity,S=maximum height
0=(64)^2-2(32)(S)
64*S=64*64
S=64 feet
therefore,max height=64 feet
If you don't know this from physics,don't worry,this can be solved by maths as well.
This we can also get using the relation given to us:

At t=0,s=-16(0) + 64(0)=0 feet
At t=1,s=-16(1)^2 + 64(1)=64-16=48 feet
At t=2,s=-16(2)^2 + 64(2)=128-16(4)=128-64=64
At t=3,s=-16(3)^2 + 64(3)=192-16(9)=192-144=48
At t=4,s=-16(4)^2 + 64(4)=256-16(16)=256-256=0
We have been asked to graph this function for (0<=t<=4).
Now as you can see,we have substituted values of 't' starting from 0 and ending at 4.
This shows us that the maximum value was at the middle,at t=2 seconds.At that time,s(height) was 64 feet.
This also means that in the first two seconds the ball rose upwards in the air,and reached its maximum at time=2 seconds,and then took 2 seconds to return back to ground.
We have only taken a few points,if you took smaller intervals of time,say you calculated value of 's' after every 0.1 seconds of 't',you would get a graph like this:
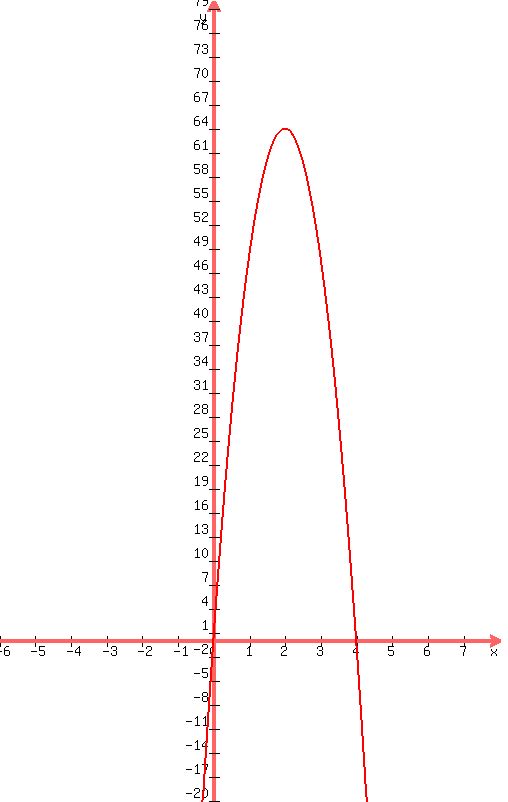
(Height on y-axis,Time on x-axis)
So thats your graph,and your max height is : 64 feet
Hope this helps,
Prabhat
|
|
|