|
Question 183218: This problem has more than one part, please HELP ME put it all together.?
The price of unleaded regular gasoline varies with the price per barrel of oil on the world market. When oil was selling for $30 per barrel I paid $1.25 per gallon for gasoline. When oil was selling for $140 per barrel, I paid $4.00 for a gallon of gasoline. I have to make a table showing the above data for gasoline and oil prices. Then, I have to construct a graph with oil price per barrel on the horizontal axis and the price per gallon of gasoline on the vertical axis, then plot the two points given and draw a line connecting the two points and extending over the range of $0 to $150 for the price of a barrel of oil, and find the slope of the line, then find the “y” intercept for the line (the point where oil is $0.00 per barrel) and finally write the equation of the line. Assuming that the relationship is linear, I have to calculate the price for a gallon of gasoline when the oil price reaches $39.34 per barrel. How does this compare to the price you are paying today?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x=price per barrel of oil and y=price per gallon of gasoline
First translation: "When oil was selling for $30 per barrel I paid $1.25 per gallon for gasoline" means that when  , ,  . So we have one point (130,1.25) . So we have one point (130,1.25)
Second translation: "When oil was selling for $140 per barrel, I paid $4.00 for a gallon of gasoline" means that when  , ,  . So we have another point (140,4) . So we have another point (140,4)
So here's the table of the two ordered pairs (points)
Now set up the axis (with the proper ranges and labels)

Plot the two points

Draw a line through the points (in blue)

-----------------------------------------------------------------
Now let's find the equation of the line that goes through the points (130,1.25) and (140,4)
First let's find the slope of the line through the points (130,1.25) and (140,4)
Note: ) is the first point (130,1.25) and is the first point (130,1.25) and ) is the second point (140,4) is the second point (140,4)
 Start with the slope formula. Start with the slope formula.
 Plug in Plug in  , ,  , ,  , and , and 
 Subtract Subtract 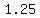 from from  to get to get 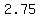
 Subtract Subtract  from from  to get to get 
 Divide Divide
So the slope of the line that goes through the points (130,1.25) and (140,4) is 
Now let's use the point slope formula:
 Start with the point slope formula Start with the point slope formula
 Plug in Plug in  , ,  , and , and 
 Distribute Distribute
 Multiply Multiply
 Add Add 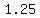 to both sides. to both sides.
 Combine like terms. Combine like terms.
So the equation that goes through the points (130,1.25) and (140,4) is 
The equation is now in slope intercept form  where the slope is where the slope is  and the y-intercept is and the y-intercept is 
Note:
Since the slope is  , this means that for every dollar increase that the price per barrel of oil experiences, the price per gallon of gas will increase $0.275 , this means that for every dollar increase that the price per barrel of oil experiences, the price per gallon of gas will increase $0.275
Also, the y-intercept is the value when the price of oil is $0 per barrel. So if the price per barrel is $0, then the price of gas is -34.50 dollars.
-------------------------------------------------------------------
"Assuming that the relationship is linear, I have to calculate the price for a gallon of gasoline when the oil price reaches $39.34 per barrel"
In this case, we want to know "y" when "x" is equal to 39.34. So simply plug in  to find "y" to find "y"
 Start with the equation we just found Start with the equation we just found
 Plug in Plug in 
 Multiply Multiply
 Subtract Subtract
So when the price of oil is $39.34 a barrel, the price of gas will be about -23.68 dollars a barrel.
Note: the relationship between the price of oil and the price of gas is a little more complex than just a simple linear relationship (since there are more factors involved).
|
|
|
| |