Question 181944This question is from textbook Algebra2
: Complete parts a-c for each quadratic equation
a) find the value of the discriminant
b) describe the number and type of roots
c) find the exact solutions by using the Quadratic Formula
14) x^2+3x-3=0
This question is from textbook Algebra2
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)
From  we can see that we can see that  , ,  , and , and 
 Start with the discriminant formula. Start with the discriminant formula.
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get 
 Multiply Multiply  to get to get 
 Rewrite Rewrite  as as 
 Add Add  to to  to get to get 
So the discriminant is 21.
----------------------------------------------------
b)
From part a), we see that  . This means that . This means that  (ie the discriminant is positive) (ie the discriminant is positive)
Since the discriminant is greater than zero, this means that there are two real solutions.
So we can say that...
Type of Solution(s): Real
Number: 2 (these are distinct)
-----------------------------------------------------
c)
 Start with the given equation. Start with the given equation.
Notice we have a quadratic equation in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for x
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get  . .
 Multiply Multiply  to get to get 
 Rewrite Rewrite 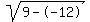 as as 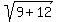
 Add Add  to to  to get to get 
 Multiply Multiply  and and  to get to get  . .
 or or  Break up the expression. Break up the expression.
So the answers are  or or 
which approximate to  or or 
Notice how there are two real solutions. So this confirms our answer to part b)
|
|
|