Question 181640: Guy Wire. How long is a guy wire reaching from the top of a 12-ft pole to a point on the ground 8 feet from the pole?
Found 2 solutions by eperette, Electrified_Levi:
Answer by eperette(173)   (Show Source):
You can put this solution on YOUR website! This is a typical right triangle problem, how should you know:
(1) Draw a figure: the pole must be straight up (leg of triangle), from the bottom of the pole to the point where the wire will connect to the floor is another leg of triangle, and the wire is slanted from top of pole to floor.
(2) You use pythagorean theorem to solve problems where (a) it is a right triangle, (b) you know two side's lenghts of the triangle and need to find missing side length.
a^2 + b^2 = c^2 ; where c is the longest side (hypoteneus, accros from 90 degree angle)
ANSWER:
a^2 + b^2 = c^2
(8)^2 + b^2 = (12)^2
64 + b^2 = 144
64-64 + b^2 = 144 - 64
b^2 = 80
sqr(b^2)= sqr(80)
b= sqr(80)
b= sqr(16*5)
b=sqr(16)* sqr(5)
b= 4sqr(5)
where sqr means square root
Answer by Electrified_Levi(103) (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
First you would draw something sort of like this, you can make it more creative, and draw the actual pole
.
.
It will look like a right triangle.
.
We are trying to find "c", Since we know that it is a right triangle, we can use the Pythagorean Theorem, which will work only with right triangles
.
Pythagorean Theorem = 
.
"a" and "b" refer to the legs of the triangle ( the horizontal and vertical lines ). I usually think of "a" as the vertical line, and "b" with the horizontal line, but it doesn't really matter.
.
All you do now is replace the variables with the numbers we know
.
=  =  =  =  , to find "c" we will take the square root of both sides
.
=  =  =  or  , a measurement cannot be negative so
.
If you wanted to be most accurate, you would simplify your answer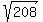 
.
You can sometimes simplify radicals if you can find factors of the number that has a whole number as a square root, in this case we can take "16" out of "208"
.
=  ( )
.
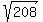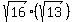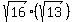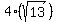=  , this is the simplified form
.
If you rounded your answer, it would be 14.42 ft
.
You can round your answer, you need to if they asked you to, but to be the most accurate, you would say the guy wire is 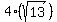 feet long, which would be your answer
.
.
Hope I helped, Levi
|
|
|
