SOLUTION: One side of a rectangular stage is 2 meters longer than the other. If the diagonal is 10 meters, then what are the lengths of the sides?

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: One side of a rectangular stage is 2 meters longer than the other. If the diagonal is 10 meters, then what are the lengths of the sides?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 181511: One side of a rectangular stage is 2 meters longer than the other. If the diagonal is 10 meters, then what are the lengths of the sides?
Answer by HyperBrain(694) About Me  (Show Source):
You can put this solution on YOUR website!
A rectangle is a parallelogram that has four right angles [rect-angle]
+++
Therefore, if we draw one diagonal, we will have two right triangles which, of course, satisfy the Pythagorean theorem.
+++
Let x=width
. x+2=length
+++
The diagonal of length 10 acts as the hypotenuse while x and x+2 are the legs. Using the Pythagorean theorem,
x2+(x+2)2=102
x2+(x2+4x+40)=100
2x2+4x+40=100
x2+2x+20=50
x2+2x-30=0
+++
Using the quadratic formula,

+++
Initially we had two values for x. However, 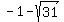-1-sqrt%2831%29 is invalid since it will yield a negative value which is impossible for there are no negative lengths.
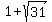Thus, x=-1%2Bsqrt%2831%29 m, x+2=1%2Bsqrt%2831%29 m. Theses values represent the sides of the rectangle.
+++
Power up,
HyperBrain!
Visit my blog move your mouse and click here