|
Question 180879This question is from textbook College Algebra a Graphing Approach
: Rental Demand:A real estate office handles an apartment complex with 50 units. When the rent per unit is $580 per month, all 50 units are occupied. However, when the rent is $625 per month, the average number of occupied units drops to 47. Assume that the relationship between the monthly rent p and the demand x is linear.
a. Write the equation of the line giving the demand x in terms of the rent p.
b. Use a graphing utility to graph the demand equation and use the trace feature to estimate the number of units occupied when the reant is $655. Verify your answer algebraically.
c. Use teh demand equation to predict the number of units occupied when the rent is lowered to $595. Verify your answer graphically.
Thanks - I'm so frustrated and have been stuck on word problems for 2 weeks. - Thanks
This question is from textbook College Algebra a Graphing Approach
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A real estate office handles an apartment complex with 50 units. When the rent
per unit is $580 per month, all 50 units are occupied. However, when the rent
is $625 per month, the average number of occupied units drops to 47.
Assume that the relationship between the monthly rent p and the demand x is linear.
:
a. Write the equation of the line giving the demand x in terms of the rent p.
:
Using the slope formula: m = 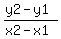 find the slope find the slope
Assign the given values as follows
x1 = 580; y1 = 50
x2 = 625; y2 = 47
m =  = = 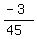 = = 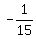
Write the equation using the point/slope formula y - y1 = m(x - x1)
y - 50 = 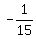 (x - 580) (x - 580)
y - 50 = 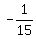 (x - 580) (x - 580)
y = 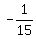 x + 38.67 + 50 x + 38.67 + 50
y = 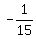 x + 88.67 x + 88.67
The way they have written it, demand (d) dependent on price (p) it would be
d = 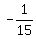 p + 88.67 p + 88.67
:
:
b. Use a graphing utility to graph the demand equation and use the trace feature to estimate the number of units occupied when the rent is $655. Verify your answer algebraically.
:
Substitute 655 for p in the above equation
d = 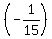 (655) + 88.67 (655) + 88.67
d = -43.67 + 88.67
d = 45 units rented at $655
:
On a TI83, it would look something like this:
(Xmin=-100, Xmax=800; Ymin=-20, Ymax=100)

:
:
c. Use the demand equation to predict the number of units occupied when the rent is lowered to $595. Verify your answer graphically.
:
Substitute 595 for p in the above equation in the same way
d = 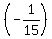 (595) + 88.67 (595) + 88.67
d = -39.67 + 88.67
d = 49 units rented at $595, verify on the same graph
:
:
they should not have assigned the demand as x. x is usually the independent
variable and here, the demand is the dependent variable. Causes confusion.
:
Hopefully, this has relieved some of your frustration, and you can enjoy the rest of this blessed Sunday! Carl
|
|
|
| |