Question 180633: Falling Objects
Given:
(object height in feet)= -16t+(initial velocity)*(time in seconds)+(initial height in feet)
If a rock were thrown on the surface of Earth with an intial velocity of 27 feet per second from an initial height of 6 feet, would it take a longer or shorter period of time to reach the ground than it would on the surface of the moon? Use the Quadratic Formula to find the actual time that the rock would remain in the air.
I am very confused. There is so much information it is overwhelming. Can you please help me set it up and solve? Thanks!
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! Equation of height of object (earth):
Because Earth gravitational pull is 32 feet/sec^2

where
y is the position of the object
t is time in seconds
.
Setting y to 0, (which is equivalent to asking when is is level w/ground)

Applying the quadratic equation we get:
y = {-0.199, 1.886}
Throw out the negative solution we get
1.886 secs in the air (Earth)
.
.
.
Similarly, for the Moon (where gravity is 1/6th that of the Earth) we have:

.
Setting y to 0, (which is equivalent to asking when is is level w/ground)

Applying the quadratic equation we get:
y = {-0.218, 10.343}
Throw out the negative solution we get
10.343 secs in the air (Moon)
.
.
.
CONCLUSION: IT WOULD TAKE LONGER FOR THE OBJECT TO HIT THE GROUND ON THE MOON.
.
.
.
Below are the details of BOTH quadratic:
Earth's quadratic:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=1113 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 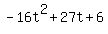 can be factored: can be factored:

Again, the answer is: -0.198801707350767, 1.88630170735077.
Here's your graph:
 |
Moon's quadratic:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=793 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 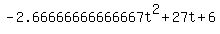 can be factored: can be factored:

Again, the answer is: -0.217547940123272, 10.3425479401233.
Here's your graph:
 |
.
|
|
|