Question 180438: The number of units, n, of a commodity sold at price ,p, is given by n= -0.2p + 50. The revenue is the product of the selling price and the number of units sold. The maximum revenue for this commodity is?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The number of units, n, of a commodity sold at price ,p, is given by n = -0.2p + 50. The revenue is the product of the selling price and the number of units sold. The maximum revenue for this commodity is?
:
We know that revenue = no. of units (n) times the price (p)
so we have:
r = p * n
given that n = -.2p + 50, substitute this for n
r = p * (-.2p = 50)
:
r = -.2p^2 + 50p; a quadratic equation
;
The max revenue occurs at the axis of symmetry, find it using: x = -b/(2a)
p = x, a =-.2, b = 50
p = 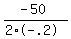
p = 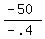
p = +125 price for max rev
:
Find the max rev by substituting 125 for p
r = -.2(125^2) + 50(125)
r = -.2(15625) + 6250
r = -3125 + 6250
r = $3125 max revenue
;
Did this make sense to you now?
|
|
|