Question 180053: In a cartoon , a malfunctioning cannon fires a hungry coyote towards the bottom of a cliff with an initial rate of 100 feet per second. If the cliff is 1250 feet tall , how long will it take the coyote to reach the desert floor? (To account for gravity, use the formula d =rt + 16t^2, where d =distance, r = initial rate, and t = time.
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a cartoon , a malfunctioning cannon fires a hungry coyote towards the bottom of a cliff with an initial rate of 100 feet per second. If the cliff is 1250 feet tall , how long will it take the coyote to reach the desert floor? (To account for gravity, use the formula d =rt + 16t^2, where d =distance, r = initial rate, and t = time.
.
From your problem, you are given:
d = 1250 feet
r = 1000 ft/sec
t is what we're looking for...
.
Plug in the provided values and solve for t:
d =rt + 16t^2
1250 = 1000t + 16t^2
625 = 500t + 8t^2
0 = 500t + 8t^2 - 625
.
Using the quadratic equation, we get:
x = {1.110, -1.126}
.
We can toss out the negative solution leaving us with:
x = 1.110 seconds
.
Details of quadratic follows:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=1250064 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 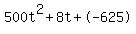 can be factored: can be factored:

Again, the answer is: 1.11006261005366, -1.12606261005366.
Here's your graph:
 |
|
|
|