|
Question 179578: Homework Question:
Find the area of the triangle enclosed by the lines,
1 . y=2/3x -7/3
2. y =-1/2x+3/2
3. y=-6x-5
Find the points of intersection and then map on a graph.
I started out by finding the x and y coordinates of each line to plot on the graph. The triangle I get is so small that I know I need to find the points of intersection but I am not sure how. Then I guess find the side length I think and lastly the area but unsure of what path to take. I am a middle grade teacher working towards my endorsement and taking class. This was the homework the teacher gave. He made it up, it did not come from a text.
I would appreciate any help you can give.
Thanks!!!
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here are the lines graphed.
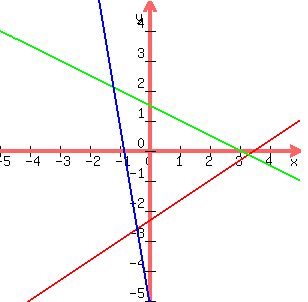
To find the points of intersection, set the equations equal to each other.



That is,



.
.
.
Here's 

Solve for x, then go to eq. 1 or eq. 2 and solve for y.
.
.
.
Next you need to decide how you'll calculate the area : Heron's formula or the traditional base-height relationship.
.
.
.
Heron's formula:
You can find all the lengths of the triangle using the distance formula,

and then use Heron's formula for triangle area.
Heron's formula uses the three sides of a triangle a,b,c and the semi-perimeter,s.

where

.
.
.
The traditional area of a triangle would give you,

where b stands for base and h is the height, the perpendicular distance from the base to opposite base vertex (altitude).

Once you have the three intersection points then you can call one side the base, let's assume the green line is the base.
Find its length with the distance formula.
Then you would need to find the altitude shown here as the red line.

Since you know the slope of the green line, you also know the slope of the red line since perpendicular lines follow this relationship,

You can then formulat the equation of the line using this slope and the intersection point opposite of the base (which you calculated previously) using the point-slope form of a line,

We'll call that equation 4.
Now you need to find the intersection point of line 4 and the green base line.
Again set the two equations equal to each other and solve for x and y.
Now that you have the intersection point, use the distance formula to find the length of the altitude.
Then use the area formula,

|
|
|
| |